Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
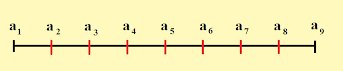
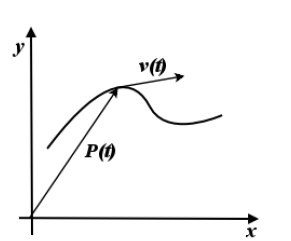
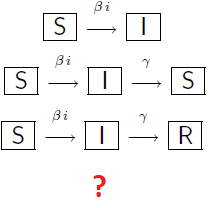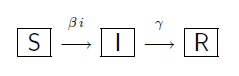Ancora un quiz semplice, ma non proprio facile. Questo dipenderà anche dal metodo di risoluzione. Comunque accessibile a tutti; non è affatto richiesta nessuna particolare conoscenza di matematica, a parte le somme di numeri naturali. Tuttavia, questo tipo di problemi è stato inquadrato in una ben nota serie.
Una soluzione alternativa a quella del quiz uova-grattacielo, esposta ieri con massima chiarezza da Vincenzo; la ricerca e la realizzazione di un algoritmo talmente semplice da poter essere compreso anche da un calcolatore. Ma alla fine a farla da padrona è pur sempre la matematica. In particolare quel ramo della stessa fondato da George Boole.
Questi facile esempio sul teorema di Ramsey mette in luce ancora una volta che il disordine completo non può esistere. Qualunque insieme di enti sufficientemente grande contiene necessariamente una configurazione molto regolare.
Finalmente una matematica accessibile a tutti: basta seguire il tag Ramsey dove sono illustrati i prerequisiti per capire uno dei teoremi più strani che io abbia mai visto, dall'enunciato semplice, che potrebbe comprendere anche un bambino. Chi vuole può seguire anche la dimostrazione che è un pò più complessa, ma anche qui non sono previste […]
Questo articolo contiene una panoramica dei tre modelli matematici trattati, applicabili ad eventi che riguardano "cose" che si trasmettono con il contatto tra individui di una popolazione. N.B.: per i dettagli , vi rimando al tag modelli matematici dove trovate per esteso tutti i calcoli. Sostanzialmente , tutto si basa principalmente sulla formula, giustificata sia statisticamente che empiricamente: […]
Purtroppo ancora un articolo tecnico; del resto per affrontare a grandi linee la dimostrazione della congettura, abbiamo bisogno di alcuni concetti di geometria differenziale. In questo articolo cominciamo ad affrontare la curvatura di una linea. E' l'esempio più facile di curvatura di una varietà; il caso n=1. La curvatura di una linea, ci servirà poi per analizzare la curvatura di una superficie, per poi astrarci al caso più generico di varietà di dimensione qualsiasi (il tensore di curvatura d Riemann).
Nel processo di riqualificazione che abbiamo descritto nel precedente articolo, sul modello SIS, si ipotizzava che la popolazione totale restasse costante. La somma delle due percentuali, Istruiti e Superati, valeva quindi costantemente 1. Introduciamo una nuova ipotesi che tenga conto di un fenomeno di “abbandono”. Vale a dire che, tra tutti coloro che periodicamente rientreranno nel circolo della […]
Ogni promessa è un debito; questa appendice vuole giustificare (con il metodo rigoroso dell'analisi) le equazioni differenziali comparse nello studio dei modelli SIS e SI. Mi dispiace, dovevo farlo prima.
Il quiz lo trovate qui. Sostanzialmente, mi sembra che Maurizio abbia imbroccato la soluzione, anche se con la sua metodologia empirico-intuitiva che secondo me lo contraddistingue. Vi dò una soluzione un po' più formale al quiz, semplice e concisa. Ho aggiunto due figure per capirci meglio , Scusate per la loro rozzezza. La domanda era questa: […]
Questo articolo costituisce il seguito all'articolo REALTÀ E RAPPRESENTAZIONE : I MODELLI MATEMATICI. NON è necessaria alcuna conoscenza delle equazioni differenziali, ma solo del concetto di derivata , e dell'integrale di 1/x , assieme alla derivata del logaritmo. Il termine equazione differenziale può spaventare; ma non è altro che una equazione dove compare una funzione incognita assieme alla sua derivata. Quindi niente di trascendentale.D'altronde , ormai la scuola superiore fornisce questi concetti sia agli istituti commerciali che a quelli professionali ; basta un po' di buona volontà per la comprensione dei calcoli che purtroppo sono alla base dei modelli. Dopo aver trattato il modello SI, tratteremo ora il modello SIS. Ma vediamo cos'è..
Può la matematica predire il futuro? Ecco un esempio di Realtà e rappresentazione , un modello matematico deterministico.
Mi sto sempre di più sforzando di scrivere quiz con domande complesse ma soluzioni molto semplici. Questa volta nessun calcolo, solo pensiero allo stato puro. Un quiz accessibile a tutti.Per chi è ostica la parola grafo, la sostituisca con "figura composta da punti e lati che li collegano". Qui la teoria dei grafi non serve a niente.
Continuiamo con questi mini-articoli non troppo impegnativi ma che servono anche per distrarci un pò. Proseguiamo verso le teorie di Ramsey con piccoli passi. Passeremo anche attraverso un altro quiz. La matematica discreta è un pò come la teoria degli insiemi; è astratta ma è semplice e affascinante, ed inoltre non richiede prerequisiti matematici profondi […]
Vorrei cambiare un po' metodo di stesura degli articoli, e farne tanti di piccole dimensioni , su cose semplici, ma che magari sfuggono alla conoscenza della maggior parte dei lettori. Non mi sono dimenticato della serie su Poincarè, ma l'articolo che sto preparando sulla connessione fra metrica e curvatura è impegnativo, e richiede molto tempo. Introduco questo […]
Posso dire di essere molto contento, in quanto quello che desideravo si è avverato; lo scopo era trovare una soluzione alternativa ad un problema molto importante per introdurre la teoria di Ramsey nel piano Euclideo. Ringrazio dunque Vincenzo per essere riuscito in tale intento; il problema non è banale anche se le soluzioni sono semplici. […]
Esiste una classe di affascinanti problemi , nell'ambito del piano o dello spazio, in cui i punti sono contraddistinti da determinate proprietà. Vedremo come questo quesito potrà servire per introdurre una importante classe di problemi di matematica discreta. Tanto per essere originali, assegneremo, ad ogni punto del piano, il metallo di cui è costituito. Diciamo che […]