Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
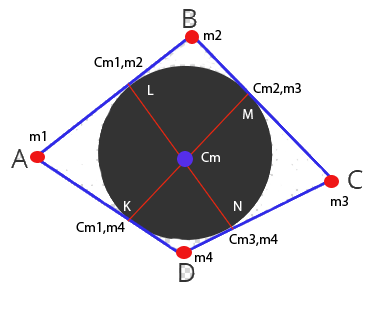
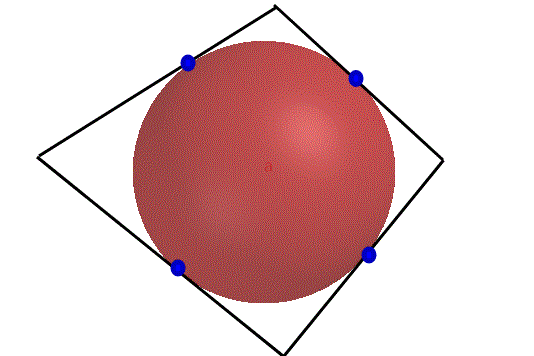
La soluzione da me proposta si basa sulle proprietà del baricentro. Si potrebbe scrivere in modo molto stringato, ma cerco di spiegarla in modo che anche in non esperti in certe proprietà vettoriali del baricentro possano comprenderla. La fisica qui non c'entra niente; lo stesso si avrebbe definendo una certa entità con operazioni da svolgere su vettori con moduli proporzionali a determinati numeri ( numeri detti anche scalari).
Sto cercando disperatamente di proporre dei quiz che siano risolvibili anche dal cellulare, quindi privi di disegni e calcoli complessi. Lasciamo per un pò perdere poi l'esposizione romanzesca, per essere più precisi, come lo vuole la matematica (anche perchè in questo caso non avrei idee per scriverla). Abbiamo a che fare con una figura sbilenca è una simmetricamente perfetta; cosa succederà ai punti di contatto se si tenta di incastrare una nell'altra?
Un articolo un po' più tecnico dei precedenti, che purtroppo presuppone la conoscenza delle derivate. Tuttavia ciò ci permetterà di sfatare definizioni e formalismi tipici della geometria differenziale, quali i tensori metrici e gli elementi di linea infinitesimi. Ricordiamoci che il nostro scopo è quello di capire come vivere all'interno di una varietà dove di euclideo resta ben poco. In ogni caso, però, tramite il piano tangente possiamo ridurci sempre ad esso.
Qui trovate il quiz e le soluzioni nei commenti. Due parole sulla soluzione, anche se non servirebbe. Intanto la giustificazione dei quattro asterischi per la soluzione completa, ovvero che il percorso indicato dall'autista è quello minimo. Questo era riservato a chi trovasse una soluzione autonoma, indipendente dal teorema di Eulero, che abbiamo visto qui. Nei […]
Sulla scia dei minimi percorsi, vi propongo questo quiz, più logico però che matematico. Nessun conto da fare, a parte delle somme e delle moltiplicazioni. Quindi aritmetica base . Probabilmente ci sono diversi modi per risolverlo, ma il più elegante riguarda degli argomenti da me trattati in questo sito. Ma chiaramente ogni altra soluzione è ben accettata. Non c'è altro da dire. So che saprete valutare da soli le risposte, mentre il testo penso sia inequivocabile . Buon divertimento!
Riporto la soluzione del quiz su Giulietta e Romeo, così come l'hanno scritta un gruppo di lettori.Affrontiamo anche in questo articolo la versione digitale; dei lucchetti matematici e delle chiavi cifrate per scambiare la combinazione di un lucchetto "fisico".
Cosa sarebbe successo a Giulietta e Romeo ai tempi nostri? Forse si sarebbero conosciuti su internet. Un quiz che mi è piaciuto per la sua semplicità, e che propongo pur sapendo che i più esperti possono esserne a conoscenza, essendo un problema classico di logica creativa. Mi auguro che chi lo conosca non partecipi alla discussione. Il problema è si semplice, ma non è detto che la soluzione sia immediata.
Se vogliamo addentrarci correttamente alla comprensione delle varietà Riemmane, abbiamo bisogno di qualche concetto riguardante argomenti di matematica avanzata, che di solito di studiano nei primi due anni di università . Chiaramente non è nei nostri scopi né nelle nostre possibilità approfondire tali argomenti. Provo perciò a presentarli in modo pratico-intuitivo, sfruttando anche il lavoro fatto da Vincenzo e da Fabrizio. Parleremo di matrici e del loro prodotto, di derivate parziali e equazioni parametriche, nonché di prodotti scalari. Spero che questo sia sufficiente per comprendere uno dei concetti più belli e potenti della matematica che è alla base delle teorie relativistiche e della cosmologia: le varietà Riemmane.
Questo articolo è la continuazione della miniserie riguardante i paradossi insiemistici, che trovate nell'archivio di matematica. Nel primo articolo abbiamo visto come la costruzione assiomatica di Zermelo-Fraenkel permette di eliminare il paradosso di Russel, e anche quello dell'insieme universale (esistenza dell'insieme di tutte le cose). Lascia però degli interrogativi; se l' "insieme" di Russel e l' "insieme universale" non sono insiemi, allora cosa sono?
Purtroppo la congettura di Poincarè non è risolvibile con gli strumenti topologici, che sono qualitativi. Abbiamo bisogno di strumenti quantitativi, per risolvere tale congettura. Perciò introduciamo in questo articolo e nel prossimo un breve riassunto sui concetti più importanti della geometria differenziale; le varietà differenziali e quelle dotate di metrica.
Nella serie "MATEMATIZZIAMO IL NASTRO DI MÖBIUS", abbiamo visto come generare delle varietà bidimensionali in modo astratto. Riprendiamo in modo meno formale tale procedimento,estendendolo allo studio delle tri-varietà,ossia le varietà di dimensione tre,che non sono rappresentabili nello spazio tridimensionale.
Qui trovate il quiz e i commenti. Presento la mia soluzione in modo un po' più formale. Questo per dare una spiegazione in più; già leggendo i commenti di Vincenzo (e anche di altri) si riesce a giustificare la soluzione in modo intuitivo-geometrico.Mi baso su una figura, che è un caso semplificato del nostro problema. […]
Nel 1901 Un lord Inglese,filosofo e matematico,Bertrand Russel, mise in crisi il tentativo di Frege di definire le basi della matematica partendo dalla logica pura, con un paradosso arcinoto a tutti. Tale paradosso era dovuto al fatto che la teoria "ingenua" ovvero intuitiva degli insiemi non era ben fondata. Questo destò grande preoccupazione nel mondo della matematica; se gli insiemi sono alla base della matematica e sono non consistenti, allora tutta la matematica potrebbe essere non consistente, ovvero contraddittoria, e si temette anche per la teoria di Cantor. Ma vediamo perchè successe tutto ciò.Nella realtà attuale, con assiomi consistenti, il paradosso di Russel diventò un teorema.
Un quiz intricato..ma che può diventare lineare.Quanto al valore didattico del quiz, possiamo dire solo che costituisce un ripasso sulle leggi della riflessione. Non solo, la sua soluzione richiede doti creative e di ingegno. La matematica necessaria per risolvere il quiz è poi veramente elementare.
Nato nel 1854, Poincaré fu l’ultimo genio mondiale di cognizioni scientifiche universali, non frenato da alcuna barriera disciplinare, forte d’una erudizione scientifica portentosa. Formulò quello che è stato il il quinto problema del Millennio, la congettura che porta il suo nome. Per non parlare del grosso contributo dato allo studio della relatività ristretta.
Eccoci dunque alla prima puntata della serie dedicata alla congettura di Poincaré. Per capire bene l'enunciato della congettura è necessario conoscere il concetto di "semplice connessione". Procederemo in modo intuitivo, aiutandoci con disegni e ragionamenti abbastanza pratici. Non tutti gli enunciati saranno dimostrati formalmente. D'altro canto, quanto fatto nella prima serie topologica dovrebbe essere sufficiente per comprendere a fondo questo articolo.