Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
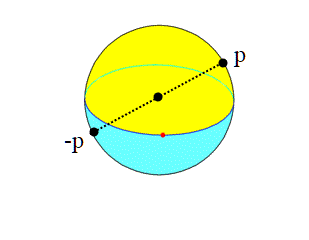
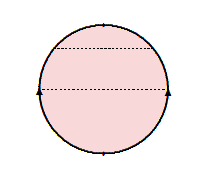
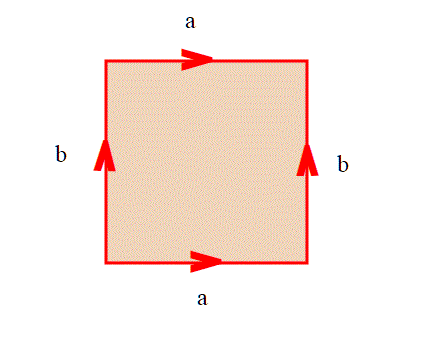
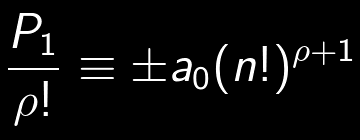Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Con l'articolo sul piano proiettivo si conclude la serie "Matematizziamo il nastro di Mobius" in cui sono stati esposti i concetti fondamentali della topologia generale. Ma lo topologia non finisce qui.Il tutto andrà poi esteso alle tri-varietà; fino ad ora ci siamo occupati di […]
In questo articolo scoprirete che il piano proiettivo è tutt'altro che un piano. Analizzeremo vari modelli di questa superficie topologica che risulta ancora più complicata della bottiglia di Klein, pur avendo con essa delle affinità.
Continua il nostra viaggio nell'affascinante mondo delle superfici ottenute con il passaggio al quoziente. Riusciremo a costruire una superficie chiusa e non orientabile, la superficie di Klein. Ma a differenza di quelle viste fino ad ora,questa superficie non esiste nello spazio tridimensionale.
Dopo tanto tempo ho deciso di proporre un quiz geometrico di una certa rilevanza. Al solito, il problema non è facile ma la soluzione sì. Difficile è inquadrarla. In ogni caso quiz richiede solo nozioni matematiche di base.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Ci sono più modi per costruire una sfera con la topologia quoziente. Il più semplice consiste però nel fare il quoziente di un disco. Fino adesso abbiamo fatto quozienti di quadrati e rettangoli, ma nulla ci vieta di farlo di altri sottospazi topologici. Consideriamo […]
Un punto d'incontro fra il toro descritto da Arturo negli articoli sulla geometria dello spazio, e il toro "topologico" ovvero descritto in modo astratto tramite la topologia quoziente. Dimostreremo in questo articolo che le due superfici sono omeomorfe.
Affrontiamo oggi i primi due esempi di superfici topologiche generate partendo dal quoziente di uno spazio topologico basilare (un quadrato o un rettangolo) . Partiamo dalle superfici più semplici da generare: il cilindro e il nastro. Fra le altre cose vedremo anche immediatamente la differenza fra superfici orientabili e non orientabili, e la definizione di orientabilità.
Eccoci arrivati alla fine della dimostrazione. Useremo ora piccole conoscenze di teoria dei numeri ,quali la divisibilità degli interi modulo Z, la fattorizzazione di un intero, e un teorema sui numeri primi già noto a Euclide, Unendo queste conoscenze ai risultati delle altre puntate, otterremo la dimostrazione di un teorema non difficile ma sicuramente molto laborioso.
Ancora un attimo di pazienza; affronteremo in questo articolo delle ulteriori elaborazioni di polinomi, e delle diseguaglianze sugli integrali. Niente di trascendentale! Ma vi assicuro che siamo prossimi alla fine della dimostrazione.
Una terza parte un po' più complessa, ma in realtà solo apparentemente. Si tratterà di lavorare in astratto su dei polinomi di grado qualsiasi. Il tutto diventerà però il fulcro della dimostrazione di Hilbert, quindi la parte più importante.
In questa seconda parte della dimostrazione della trascendenza del numero di Nepero, imposteremo una dimostrazione per assurdo. Per adesso niente di difficile, solamente dei calcoli che coinvolgono degli integrali, ma molto semplici.
Proviamo (a piccoli passi) ad affrontare una dimostrazione della trascendenza del numero di nepero. In questa prima parte ci limiteremo al calcolo di una importante proprietà della funzione Gamma di Eulero, che sarà il punto chiave di questa dimostrazione dovuta ad Hilbert.
Volevo fare un esempio semplice per applicare gli ultimi risultati (più uno inserito al volo) alla costruzione di un omeomorfismo fra uno spazio quoziente ed un sottospazio definito da una espressione analitica. Questo ci darà un metodo generale per studiare le superfici quoziente e rapportarle a quelle dello spazio Euclideo,
Un articolo al di fuori della serie topologica, ma necessario per continuare le nostre costruzioni sul quoziente topologico. Vedremo come dimostrare che l'intervallo chiuso in R è uno spazio compatto. In realtà , la dimostrazione riguarda più l'analisi matematica che la topologia.
Lo scopo di questo articolo è quello di chiarire per bene cosa sono gli spazi quoziente, e come siano collegati ad altri spazi che conosciamo molto bene. Il collegamento è realizzato tramite il concetto più importante della topologia: l'omeomorfismo. Questo teorema diventa necessario per realizzare degli omeomorfismi fra spazi topologici derivanti da una operazione di incollatura, ovvero di passaggio al quoziente.
Non è proprio banale costruire un atlante per una varietà topologica. Per cui voglio fare un esempio "pratico", usando una varietà unidimensionale; Il cerchio è infatti una varietà topologica di dimensione 1.La scelta ovviamente è per comodità grafica e di notazioni.