Dopo la dimostrazione dell'irrazionalità di π ecco quella del numero di Nepero. La dimostrazione è la più semplice che ho trovato, e si basa sostanzialmente sugli sviluppi in serie di Taylor con resto di Lagrange.
About: Umberto Cibien
Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
Recent Posts by Umberto Cibien
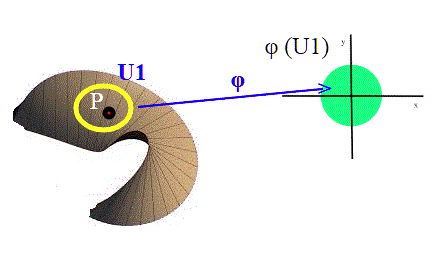
In questo articolo dobbiamo sforzarci per capire bene la differenza fra "locale" e "globale"; una superficie, o più in generale. una varietà topologica, è localmente simile ad uno spazio euclideo, ma quasi sempre non lo è globalmente. Il concetto di simiglianza viene tradotto molto bene dagli omeomorfismi.
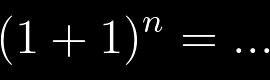
Adesso che conosciamo la formula del binomio di Newton, possiamo affrontare delle simpatiche applicazioni, che volevo proporre sotto forma di quesiti, comprensivi di soluzione. Chi vuole può provare da solo senza nemmeno entrare nell'articolo. problema:
Dato un insieme di n elementi, quanti sono i suoi sottoinsiemi? Risolvere usando la formula del binomio di Newton.
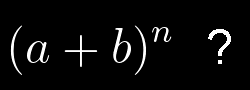
Il teorema binomiale è difficile da affrontare per la prima volta, in quanto presuppone delle conoscenze di calcolo combinatorio, in particolare delle combinazioni semplici, che spesso non sono note a tutti. Qui provo a darne la dimostrazione cercando di bypassare il calcolo combinatorio, usando anagrammi e permutazioni,oltre a nozioni base di algebra dei monomi.
Grazie alla topologia quoziente saremo in grado di costruire degli spazi topologici nuovi e molto interessanti, tipo appunto il nastro di Möbius. Si, siamo arrivati al dunque, ma ancora un attimo di pazienza. Le costruzioni che faremo ci faranno capire l'importanza in matematica delle relazioni di equivalenza, con le quali è possibile perfino "incollare" dei punti di uno spazio topologico.
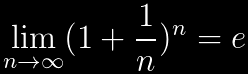
Un problema non troppo facile anche se noto. Completo di soluzione spiegata nei minimi particolari. Chi non vuole leggere la soluzione e scriverne una autonoma, si fermi pure alla scritta rossa. Sono sicuro che i nostri risolutori troveranno qualcosa di alternativo.
Ho lasciato passare un po' di tempo prima di andare avanti con la Topologia. E' ora di concludere con i concetti iniziali, ed affrontare nozioni più avanzate che ci porteranno alla matematizzazione del nastro.
No, non sto parlando dei mondiali di calcio. Forse non tutti sanno (e io l'ho saputo ieri) che mercoledì 1° agosto Alessio Figalli, matematico italiano di 34 anni, professore al politecnico di Zurigo,ha vinto la medaglia Fields, spesso descritta come “il Nobel della matematica”.
Il quiz richiedeva di calcolare la probabilità di uscire sano e salvo dall'Hotel per l'ubriaco . Riporto lo lo schema del quiz: Vorrei per prima riportare la soluzione di Fabrizio, per quanto riguarda il calcolo di tale probabilità. Penso non abbia bisogno di ulteriori commenti: Partendo dalla sala S1 ci sono 3 esiti possibili per l’ubriaco: 1) […]
Ricordate il nostra simpatico ubriaco alle prese con le chiavi del portone? Ebbene adesso il nostro amico sta affrontando un impresa ben più difficile: uscire sano e salvo da un Hotel in cui si è intrufolato per ubriacarsi gratuitamente. Fingendosi un cliente e quindi con addebito sul conto della camera di qualche sventurato, egli passa parecchio tempo […]
Uno strano quesito che si è poi rilevato un complesso esercizio di analisi matematica. Di certo interessante, perchè rimembra concetti quali i limiti, i rapporti incrementali,le derivate e un importante teorema sul valor medio di una funzione.
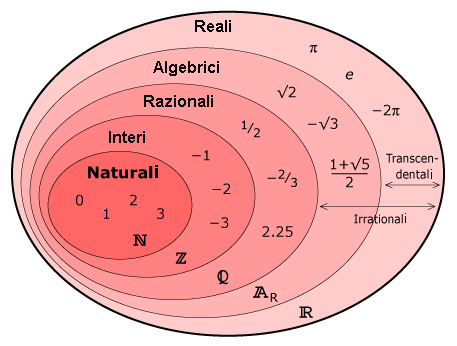
Riprendo in sintesi quanto fatto nella prima parte dell'articolo. Si definiscono numeri trascendenti quei numeri reali che non sono algebrici, ovvero non sono soluzione di alcuna equazione algebrica a coefficienti interi. Cantor riusci a dimostrare che i numeri trascendenti sono infiniti, anzi sono più che numerabili.
Dopo un quiz rilassante.. un quiz che può portare al manicomio! La domanda è difficile ma in realtà la soluzione è semplice. Bravo comunque chi lo risolve.
Prima di dare una soluzione, due spiegazioni: Il quiz tratta solo numeri positivi semplicemente perchè è nato così. Abbiamo visto varie volte che le estensioni dei quiz non sono mai troppo gradite da nessuno. Sincaso, si può fare un altro quiz. Che il quiz sia stato definito rilassante, era solo collegato al fatto che poteva essere […]
Vista la calura, un quiz non troppo difficile , ma nemmeno troppo facile. Sono però sicuro che verranno fuori in ogni caso discorsi interessanti. Speriamo che sia veramente rilassante.
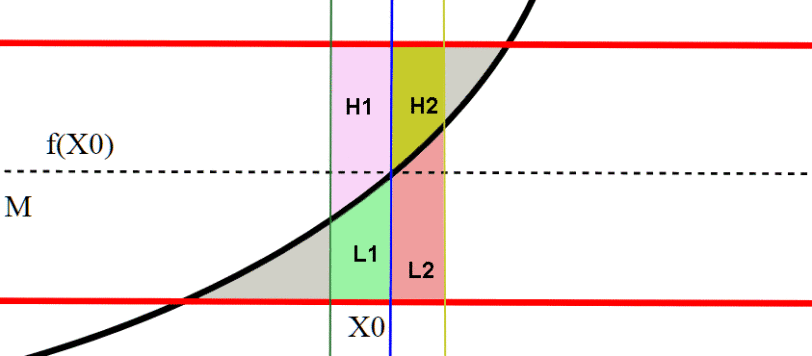
Ecco la soluzione (o meglio le soluzioni) al quiz "Diabolico" . La mia, che è di tipo geometrico-variazionale, non si discosta di molto da quelle di Vincenzo, Fabrizio, e dalle idee proposte da Mauro, Maurizio, Leandro. Diciamo che noi si siamo dannati un po' di più con i disegni, che sono però essenziali in questo caso.
Diversa invece è la soluzione di Arturo, che si basa sul calcolo differenziale-integrale.