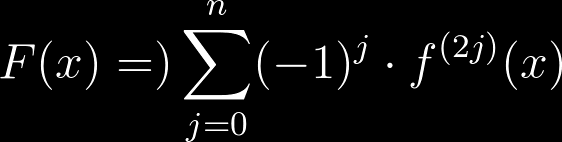Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
Perchè diabolico? perchè la sua concezione sembra stata ispirata dal diavolo. Tipo una domanda posta ad un Faust-matematico per salvare l'anima. Un quiz apparentemente difficile, ma dalla soluzione semplicissima. Ognuno può seguire vari ragionamenti.. e potrebbero anche non servire calcoli complicati.
Diciamo che il quiz presentato questa volta era un po' misterioso. Lo scopo era di parlare un po' delle stranezze dei numeri irrazionali. Tali numeri non hanno importanti proprietà gruppali come gli interi e i razionali; non c'è infatti chiusura rispetto alle operazioni di somma e prodotto. La somma di due numeri irrazionali non è sempre irrazionale..
Un quiz un po'.. fuori dal comune. Di solito i quiz hanno una soluzione, e qualche diverso metodo per arrivarci. Qui no.. secondo me le soluzioni sono veramente tante.. oserei dire .. infinite! E' un quiz infatti che lascia molta libertà di pensiero e fantasia matematica!
In questa miniserie in due puntate, scopriremo come Cantor predisse l'esistenza dei numeri trascendenti senza conoscerli direttamente, ma applicando solo considerazioni sugli insiemi infiniti.
Nell'immagine: il primo numero trascendente scoperto da Liouville.
Il quiz, che trovate qui, richiedeva di confrontare e , senza far uso di calcolatrici. In pratica, non usando le espressioni decimali di tali logaritmi. Cerco di spiegare nei dettagli la soluzione di Fabrizio, che comunque è perfetta, ma forse non tutti i lettori possono capirla al volo. Intanto ricordo che sia nel caso del logaritmo in base […]
Scusate se mi permetto di scrivere un quiz che ha come argomento i logaritmi.. ma in fin dei conti penso che almeno la definizione di logaritmo la conoscano tutti. In fin dei conti qualsiasi scuola media-superiore li tratta . E a dir la verità restano impressi. Per risolvere il quiz è sufficiente conoscere solo la […]
Il quiz è stato ampiamente risolto come potete vedere nei commenti. Propongo qui una dimostrazione leggermente diversa, che però richiede delle conoscenze che forse tutti non hanno. Il bello di questo quiz era appunto il fatto che poteva essere risolto anche usando solo la matematica elementare. La nostra trattazione richiederà una infarinatura delle classi di resto […]
Ancora un quiz che non richiede particolari conoscenze matematiche; tutti lo possono risolvere pur non essendo affatto semplice. Visto e considerato che i quiz "numerici" sembrano più graditi .. continuiamo per questa strada.
Non ce ne sarebbe bisogno, perchè il quiz è stato ampiamente risolto. Comunque, se qualcuno non avesse capito bene i passaggi li faremo uno ad uno. Il quiz richiedeva di trovare il numero civico del negozio, sapendo che la somma dei civici che lo precedono (dallo stesso lato) fosse uguale alla somma dei civici che […]
Un quiz che stavolta non richiede conoscenze matematiche avanzate (niente derivate e funzioni). Potrebbe però essere molto utile il risultato di un miniquiz visto un po' di tempo fa.
Ho voluto giustamente scrivere osservazioni e non soluzione perchè qui non stiamo parlando di matematica, ma di un giochetto atto a misurare l'abilità logico-numerica, una sorta di test. Cominciamo dall'inizio: ho volutamente usato il testo originale del quiz, senza aggiungere nessun commento o spiegazione. Il testo, così come è arrivato sul mio cellulare è il […]
Che π fosse un numero irrazionale, era già stato intuito migliaia di anni fa. Ma la prima vera dimostrazione risale al 1770, ed è dovuta a Johann Heinrich Lambert (1728-1777). Successivamente furono date altre dimostrazioni. Quella che
vedremo sembra attualmente la più semplice ed è stata data nel 1946 da Ivan Niven (1915-1999).
Cambiamo un po' stile e andiamo direttamente su WhatsApp.. Un quiz dedicato veramente a tutti (lettori e non) che non abbisogna di nessuna cultura matematica o fisica avanzata. Magari potrebbe essere la strada giusta. Chissà..
L'idea iniziale era di proporre sotto forma di quiz i prerequisiti necessari per poter comprendere un noto teorema che per ora tengo ancora nascosto. Purtroppo vista la scarsa partecipazione, ho deciso di non proporre l'ultimo quesito e risolverlo direttamente. Non vorrei tediare ulteriormente i lettori che cercano altri tipi di quiz.Ciò non toglie che chi ha in mente una soluzione migliore può scriverla tranquillamente nei commenti.
Parlare di Topologia senza parlare di spazi connessi è assurdo. Ho perciò dovuto introdurre due articoli sulla connessione. Poi potremo vedere come matematizzare il nastro, ovvero scoprire cosa significa "incollare" in senso matematico.
Continuiamo con questi mini-quesiti che una volta messi assieme comporranno la dimostrazione di un famoso teorema nell'ambito della teoria dei numeri. Vi prometto che siamo quasi alla fine, potrebbe essere la penultima puntata. Questo miniquiz è un po' più facile dei precedenti, ma è essenziale per risolvere l'obiettivo finale, che per ora tengo ancora nascosto.