Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
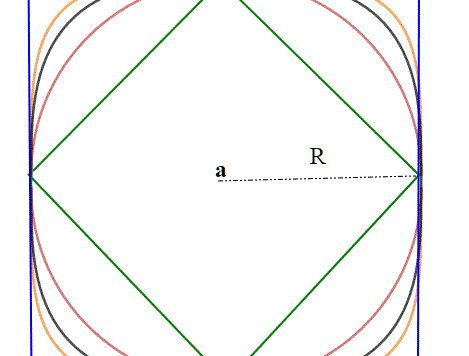
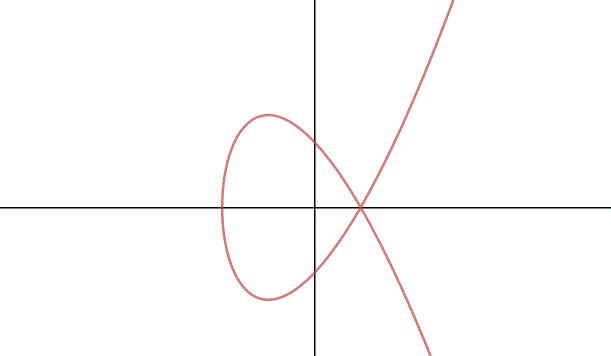
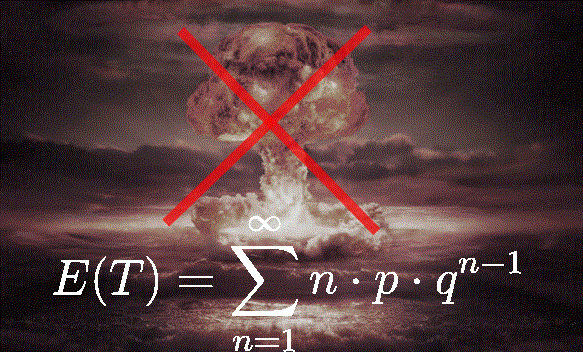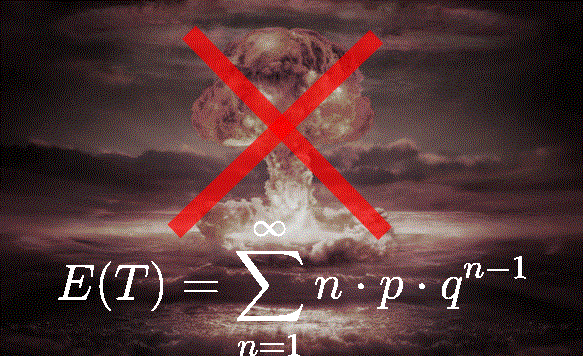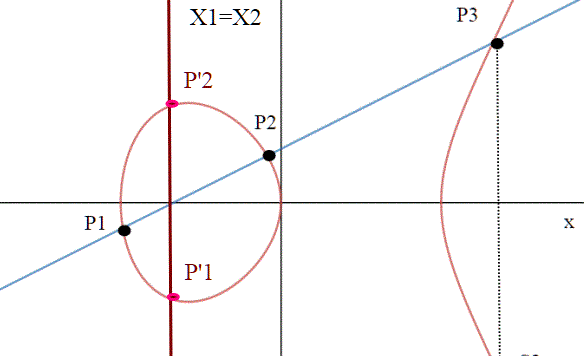Questo quiz è stato introdotto come preludio allo studio degli spazi metrici. Uno spazio metrico è un insieme di punti (e può essere anche quello euclideo) , in cui è stata introdotta una definizione di distanza,anche chiamata metrica.Prima di continuare, mi sembra doveroso dire quali proprietà deve avere una distanza. 1) d(P1,P2)>=0 (La distanza è […]
Un quiz non estremamente difficile e affrontabile penso da tutti. Richiede solo un po' di fantasia. Servirà inoltre ad introdurre un nuovo argomento: la Topologia.
... il matematico K.L.Chung arriva alla conclusione che si perviene ad un certo equilibrio fra le superpotenze dotate di ordigni nucleari poichè l'operazione di attacco diviene egualmente rischiosa per entrambe. Sappiamo invece che queste azioni di forza sono state invece compiute verso nazioni che usano armamenti di tipo convenzionale, e sprovviste di armamenti nucleari.
Già durante la seconda guerra mondiale, con le innovative armi belliche, era nata la necessità di avere dei consulenti esperti di calcolo delle probabilità ai vertici del comando. K.L.Chung, un matematico cinese, scriverà successivamente perché la matematica sia stata un deterrente per l'ipotesi di un possibile conflitto nucleare.
I problemi riguardanti il calcolo delle probabilità possono essere molto difficili, ma la loro risoluzione può essere intuitiva, e fare a meno di complesse basi teoriche. Questo lo hanno dimostrato i risolutori.
Un quiz sul calcolo delle probabilità, di esposizione brevissima, ma concettualmente non proprio semplice.
Il topo si salverà?
Se nella prima parte abbiamo concluso che scrivere la Divina commedia tramite una scimmia dattilografa non è un evento impossibile, vediamo adesso di dare una stima del numero di tentativi, e quindi del tempo necessario per raggiungere tale risultato.
Può una scimmia dattilografa e tenace , pestando a caso su una tastiera di un computer, scrivere un poema come la Divina commedia? Ebbene si, ma si può anche intuire che questo non è il miglior sistema per scrivere poemi, a meno che la scimmia non sia particolarmente longeva..
Una applicazione del'assioma della scelta porta ad una situazione paradossale; non tutti gli insiemi possono essere misurati. Lo ha dimostrato Vitali .
Un riassunto su tutto quello che abbiamo visto sulle curve ellittiche,quiz compresi, che ci porta a concludere che esse costituiscono un gruppo con una particolare operazione interna. Questo fatto è fondamentale per l'impiego delle curve ellittiche in crittografia.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Riprendiamo il discorso sulle curve ellittiche; nell' articolo precedente (qui), abbiamo trovato il punto all'infinito di una curva ellittica di equazione generica: ; esso coincide con il punto all'infinito dell'asse delle y; questo ci fa capire che la curva all'infinito è tangente all'asse delle y. […]
Se vogliamo parlare in modo totalmente corretto di equazioni ellittiche e di gruppi ellittici dobbiamo farlo all'interno del piano proiettivo. E' necessario introdurre il concetto di punto improprio o punto all'infinito, con una trattazione non strettamente formale, ma più che altro intuitiva.
In questo articolo finiamo la nostra (breve) trattazione sui numeri complessi; lo scopo è quello di fornire i strumenti minimi i calcolo che ci permettano poi di affrontare argomenti più complicati. Parleremo delle elaborazioni di due grandi personaggi della matematica: Newton e Eulero.
Per gli sviluppi delle nostre matematiche pure è necessario conoscere i numeri complessi, che forse non tutti hanno avuto la fortuna di studiare.I numeri complessi sono forse i numeri più affascinanti della matematica. Essi trovano applicazione in varie branchie della fisica (basti citare l'elettrotecnica e la meccanica quantistica). I primi scritti sicuri sui complessi sono attribuiti a Carl Friedrich Gauss (1777, 1855) la mente più privilegiata della matematica moderna.
Ho voluto fare un esempio di applicazione dei gruppi ciclici e dei campi su Zp (interi modulo p) per far capire che anche questa matematica un po' strana ha una applicazione fondamentale nella gestione della sicurezza delle informazioni. Senza saperlo, ogni volta che usiamo la carta di credito, usiamo anche i gruppi algebrici.
Per analizzare correttamente le equazioni algebriche sotto nuovi punti di vista (tipo quelle ellittiche usate da Wiles per la dimostrazione della congettura di Fermat) bisogna avere a disposizione una nuova struttura algebrica: il Campo. Nell'immagine Euclide; i suoi algoritmi sono ancora attuali perfino nelle moderne congetture matematiche.