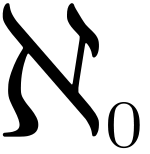Sono nato a Belluno nel 1960, dove vivo attualmente. Ho inizialmente intrapreso gli studi universitari in Informatica, per poi passare alla facoltà di matematica. Lavoro nel campo dell'informatica, come sviluppatore software in vari linguaggi di programmazione. Ma la mia vera passione resta la matematica pura. Sto cercando di divulgarla scrivendo articoli alla portata di tutti e cercando di usare il minimo formalismo. Il mio obiettivo è quello di rendere più simpatica la tanto odiata matematica che a volte ci è stata propinata come un ammasso informe di tecniche di calcolo senza alcun riferimento storico-culturale, oltre a quello di far conoscere a tutti dei concetti che sembreranno appartenere più alla filosofia che alla scienza vera e propria.
Qual'è la cardinalità del piano? A occhio e croce ben di più di quella della retta, che ha cardinalità c, pari dunque a quella dei numeri reali. Invece avremo una gran bella sorpresa: la cardinalità del piano è uguale a quella della retta. Questo fatto è fortemente controintuitivo. Lo stesso Cantor , in una lettera a Dedekind ,dove ne riporta la dimostrazione, scrive: "Lo vedo, ma non lo credo".
Nell'articolo precedente abbiamo parlato di generatori di gruppi e di gruppi liberi. Vogliamo ora provare l'esistenza di questi gruppi, senza ricorrere ad un esempio "reale", ma costruendo un gruppo libero partendo da un insieme qualsiasi. Notiamo così ancora una volta che la matematica non è solo una scienza logico-deduttiva, ma soprattutto creativa,costruttiva.
Gli articoli di Enzo spesso accendono la curiosità verso aspetti della fisica che si incontrano raramente nella comune divulgazione. È successo a me con la Lagrangiana.
In questi articoli metto in comune con il circolo quello che ho capito di questo, per me, misterioso oggetto che è stato concepito da Lagrange più di due secoli fa e che non cessa di avere un ruolo importante nella fisica moderna.
Per impedimenti tecnici non ho potuto caricare l'articolo dal mio account. Ci ha pensato Umberto che ringrazio per essersi gentilmente sobbarcato questa attività.
Ciao amici terricoli! Mi chiamo Quazel, provengo da un piccolo pianeta con due Soli situato in quella zona di cielo che voi chiamate costellazione dell’Aquila, e sono appena arrivato sul vostro pianeta! Dopo essermi sottoposto con pazienza a tutti i test preparati dai vostri scienziati e averli brillantemente superati (se non ci credete, leggete QUI), […]
Tanto per cominciare vorremmo ringraziare tutti i partecipanti, per la sottigliezza delle risposte che sono andate avanti per un bel po' tramite eufemismi, permettendo così a tutti di poter ragionare in modo autonomo. E un grazie particolare a Pippo, Leandro, Maurizio, 2*Paolo per le interessanti integrazioni alle risposte (spero di non dimenticarmi di nessuno). Questa […]
Era il 6 maggio 2054, una bella giornata di sole, quando, a bordo di un “normalissimo” disco volante (ebbene sì, proprio uguale ai dischi volanti che da sempre vediamo nei fumetti e nei cartoni animati) avvenne ciò che, ormai da tempo, ogni terrestre si aspettava accadesse da un momento all’altro: il primo contatto con un essere alieno!
Questo articolo è un po' più difficile di quelli trattati finora, richiede una buona capacità di astrazione. Vedremo come generare un gruppo partendo da un insieme qualsiasi. Qualcuno si chiederà a cosa può servire una cosa del genere.. vi anticipo solo che è fondamentale per comprendere uno dei più importanti paradossi della matematica moderna, quello di Banach-Tarski.
Una soluzione numerica del problema del missile, preparato da Pippo con l'aiuto di Umberto...
Proseguiamo lo studio dei gruppi, analizzando due gruppi fondamentali costruiti su Z; La classe di resti modulo n e il gruppo prodotto. Poi la verifica del fatto che anche le trasformazioni di Lorentz formano un gruppo.
Questo articolo porta il nome del solo Umberto, ma, in realtà è stato elaborato completamente da Fabrizio e da Umberto che hanno ottenuto, indipendentemente, la stessa soluzione. Enzo ha solo aggiunto qualche pezzetto come collante. Una piccola sorpresa nell'ellissi di minimo periodo, ma un esercizio di sicuro valore. Grazie quindi, a nome di tutti, A FABRIZIO e UMBERTO, veri artefici dell'opera d'arte!
Continuiamo il nostra percorso nei prerequisiti fondamentali sulle matematiche pure. Dopo esserci occupati di relazioni di equivalenza, fondamentali in ogni settore delle matematiche astratte, e di funzioni biunivoche (definizione di numero cardinale) ci occuperemo di una struttura molto nota e molto usata nella matematica moderna, quella di gruppo.
In questo articolo ci proponiamo di dare la definizione di numero cardinale usando il concetto di classe di equivalenza visto nell'articolo precedente. Ne approfittiamo anche per introdurre la funzione inversa e la funzione composta di una funzione, a complemento di quanto già visto nell'articolo su corrispondenze e funzioni.
Le relazioni e le classi di equivalenza aprono un altro capitolo estremamente importante della teoria degli insiemi. Tramite le classi di equivalenza è stato possibile formalizzare correttamente le definizioni di numero intero, razionale ed altro ancora. In poche parole costruire una base solida della matematica.
Sta per finire il viaggio nel paradiso di Cantor, mancano pochi articoli per la conclusione .Per cui sto già pensando a dei nuovi argomenti molto interessanti che riguardano la matematica (se si può dire) moderna. Se con Cantor ce la siamo cavata con poche nozioni sugli insiemi, introducendo di volta in volta concetti che bene o […]
La congettura che ogni insieme può essere ben ordinato presupposta da Cantor , fu dimostrata da Zermelo con il teorema sul buon ordinamento. Tale teorema ci porta immediatamente ad un'importante conseguenza; gli ordini d'infinito di due insiemi qualsiasi sono sempre confrontabili.
Il teorema di Zermelo afferma che ogni insieme può essere bene ordinato. Questo va dimostrato con il lemma di Zorn, che deriva dall'assioma della scelta. Georg Cantor considerava che questo enunciato fosse un "fondamentale principio del pensiero". Il lemma di Zorn (oppure l'equivalente assioma della scelta) ha anche conseguenze che possono apparire paradossali, come ad esempio il cosiddetto paradosso di Banach-Tarski.