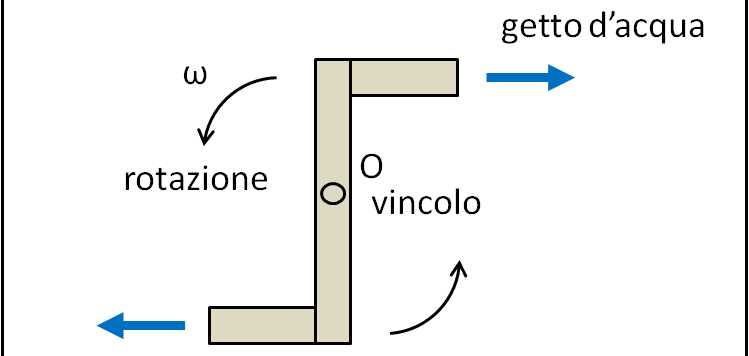
Quando Feynman era studente universitario riusciva già a proporre problemi di non facile soluzione. Uno di questi gli costò, però, il divieto di entrare nel laboratorio dell'Istituto. La fece proprio grossa...
About: Vincenzo Zappalà
Professore ordinario di Astrofisica, oggi in pensione. La sua specializzazione è stata la Planetologia e, in particolare, i corpi minori del Sistema Solare. E' stato uno dei "pionieri" dello studio fisico degli asteroidi negli anni '70, dedicandosi soprattutto alla determinazione dell'asse di rotazione e, più in generale, all'evoluzione collisionale della fascia principale. I suoi contributi hanno toccato vari risvolti innovativi sia di dinamica che di fisica, portando alla determinazione univoca, ormai globalmente riconosciuta, delle famiglie asteroidali. Su queste ha svolto studi molto dettagliati. Ha al suo attivo più di 250 lavori pubblicati sulle maggiori riviste internazionali del settore. E’ stato varie volte membro di Consigli Scientifici di Congressi Internazionali, oltre che Presidente di alcuni di questi. Ha tenuto numerosi discorsi invitati in tutti i maggiori centri di ricerca europei e americani, oltre che in Giappone, in India e in Russia (presso l’Accademia delle Scienze di Mosca). Ha tenuto un corso di planetologia avanzata presso l'Università di Rio de Janeiro. Dal 1997 al 2000 è stato Presidente della Commissione 15 dell’Unione Astronomica Internazionale, di cui è membro fin dal 1975. E’ stato anche co-leader del gruppo di lavoro sul Sistema Solare della missione spaziale GAIA. L’asteroide 2813, scoperto nell’Osservatorio Lowell di Flagstaff (Arizona), gli è stato dedicato e porta il suo nome. Ha sempre avuto una grande passione per la divulgazione, cercando di far conoscere l'astrofisica e le sue meraviglie a tutti coloro dotati di volontà di imparare, indipendentemente dal titolo di studio e dall'età. E' autore di diversi libri dedicati all'Universo.
Recent Posts by Vincenzo Zappalà
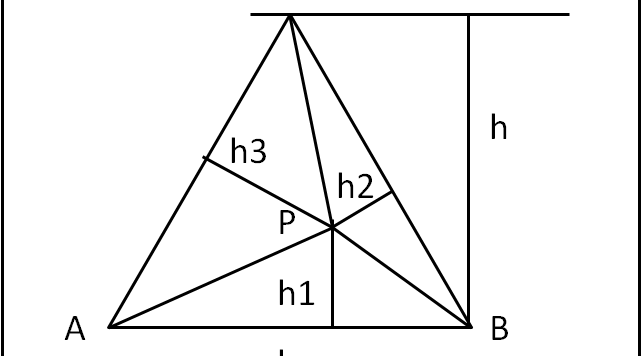
Un banalissimo e ovvio teorema (teorema di Viviani) permette di calcolare velocemente, solo per via geometrica, la probabilità richiesta.
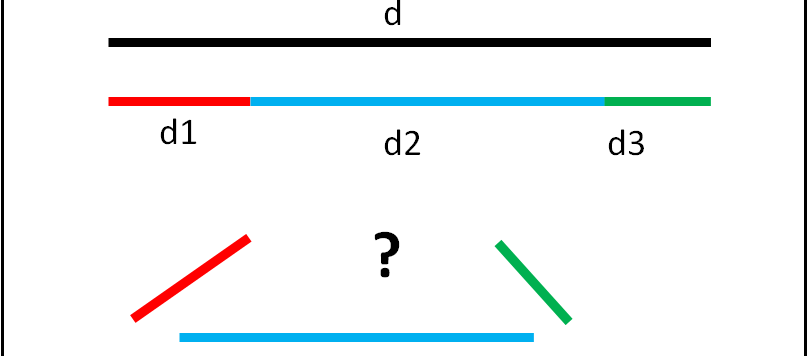
Un simpatico quiz sulla probabilità di tagliare un segmento e ottenere un triangolo. La via puramente geometrica insegnerà un teorema poco conosciuto, ma semplicissimo.
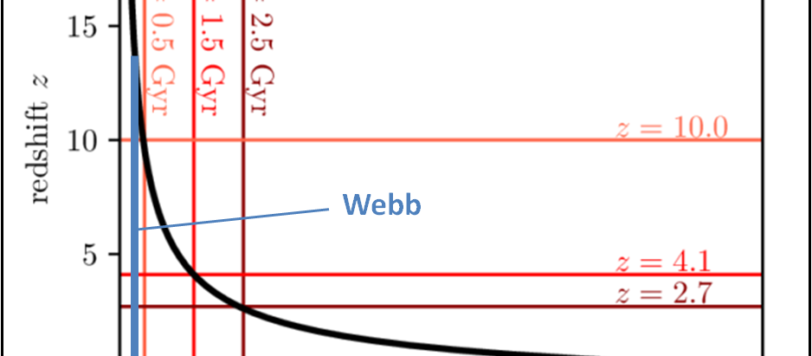
Cerchiamo di fare un po' di chiarezza sul redshift e sulle capacità di Webb. Il tutto nasce da un suggerimento del nostro amico Frank che ha giustamente notato un po' di confusione sulla rete. Speriamo che questo articolo-ciliegina serva a dare una spiegazione qualitativamente sufficiente.
Ebbene sì, anche Mimas ha un oceano sotto la sua superficie ghiacciata e profondamente craterizzata. Un oceano estremamente giovane, non più vecchio di 25 milioni di anni. Un'occasione fantastica per lo studio della nascita della vita e speriamo che in questo mondo sempre più privatizzato si riesca a capirne l'importanza.
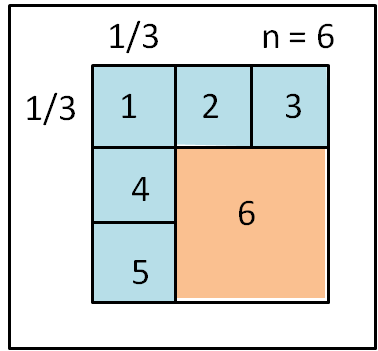
Ho cercato di usare essenzialmente il ragionamento logico, evitando qualsiasi formula, anche se semplice.
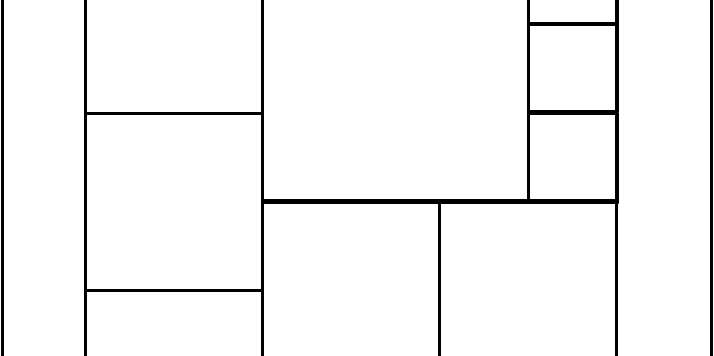
Un esercizio apparentemente geometrico che però si basa sulla logica...
Continuo con esercizi di geometria piuttosto simpatici. In questo periodo un po' caotico non riesco a fare di più... Chi ama la geometria può trovare interessante l'ultimo commento di Andy.
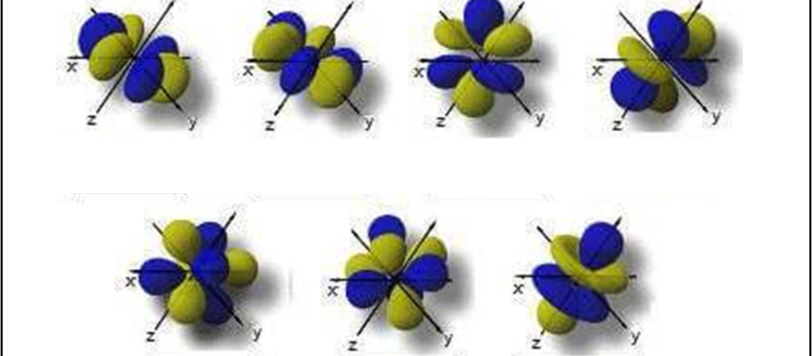
Lasciamo da parte il nucleo e spostiamoci verso l'esterno inserendo gli elettroni nei loro orbitali. In pratica, descriviamo il modello quantistico dell'atomo.
Un esercizio che poteva, come sempre, essere risolto in vari modi. Mi compiaccio con Giorgio, Andy, Giorgio, Leandro e Maurizio. Io ho voluto aggiungere un pizzico di trigonometria...
Concludiamo la nostra trattazione molto semplificata introducendo i colori, gli anticolori e il meccanismo utilizzato per lo scambio di colore tra quark, quello che origina l'interazione forte. Infine viene spiegato come nessun quark può essere osservato isolato.
Un quiz sicuramente facile, almeno nella prima parte. La seconda richiede un po' d'impegno in più.
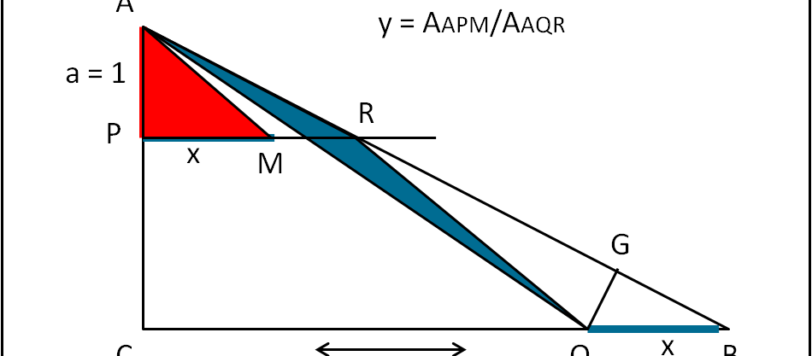
Ernesto (oltre che Andy, ovviamente) hanno risolto il quiz. Tuttavia, benché risolto in modo molto semplice si può ancora velocizzarlo. Basta ricordare che l'area di un triangolo è uguale a 1/2 del prodotto di un qualsiasi lato per la relativa altezza.
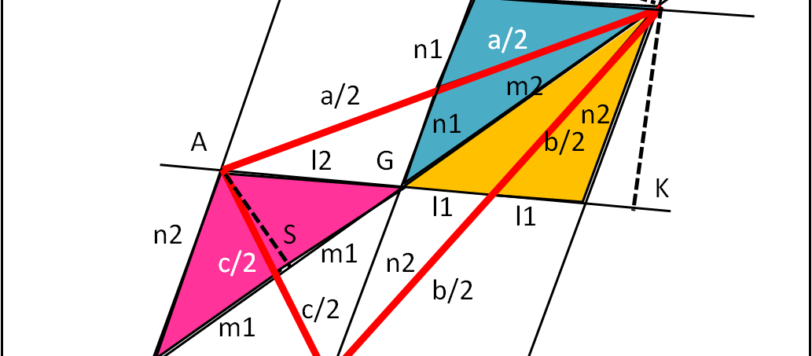
E' inutile ripeterlo: io mi diverto a inventare costruzioni geometriche e risolvere teoremi in modo non monotono e noioso. Ecco come una semplice rotazione può portare velocemente a dimostrare due teoremi relativi alle mediane di un triangolo qualsiasi.
Un quiz geometrico estremamente semplice che necessita di un minimo di ragionamento. Sia dato un triangolo rettangolo ABC, retto in C. Sul cateto AC fissiamo una lunghezza unitaria AP. Da P tracciamo la parallela a CB che incontra l'ipotenusa AB nel punto R. Consideriamo un punto Q qualsiasi sul cateto CB e sia QB = […]
Questo articolo e il successivo vorrebbero farci entrare di nascosto e in modo molto cauto nella Cromo Dinamica Quantistica (QCD), simile alla Elettro Dinamica Quantistica (QED) che studia i legami tra cariche elettriche.