Una soluzione alternativa all'esercizio risolto dai valorosi Andy e Sprmnt21.


Un semplice problema di cinematica che ci permette di colpire il nemico mentre sale su una collina.

Un telescopio che dovrebbe illuminarci sulla materia ed energia oscura ha cominciato ad illuminarci con miliardi e miliardi stelle vagabonde.
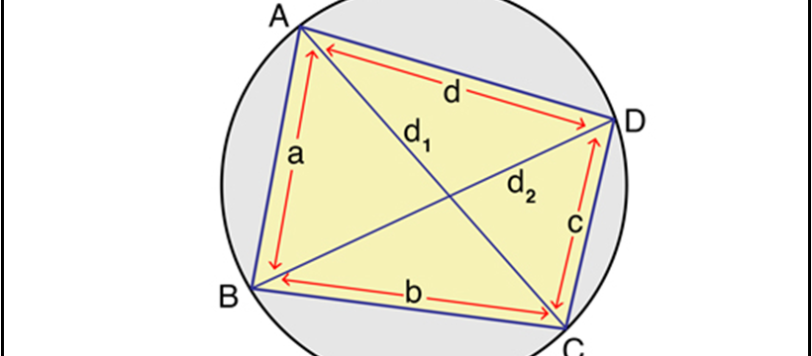
Vi è in geometria una formula non molto nota che consente di calcolare il raggio della circonferenza circoscritta ad un quadrilatero ciclico: la formula di Parameshvara, che prende il nome dal matematico e astronomo indiano Vatasseri Parameshvara Nambudiri (Kerala, India c. 1380–1460). La sua dimostrazione non è particolarmente difficoltosa in quanto si basa essenzialmente su […]

Un quiz che serve per introdurre un paio di teoremi poco conosciuti. Sempre che non siate voi a introdurli fin dall'inizio...

L'accoppiata JWST-Einstein ancora una volta permette di sbirciare tra i segreti dell'universo. E le sorprese continuano....
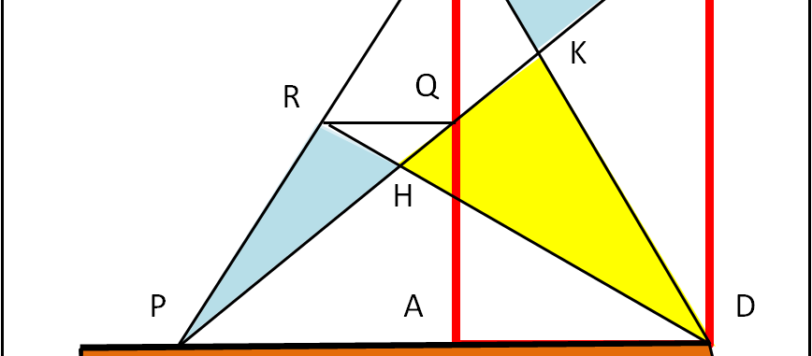
Un'avventura geometrica abbastanza curiosa che potrebbe, però, non essere lontana dalla realtà futura...

Un articolo che vorrebbe fare il punto della situazione e che è, nel contempo, una delle mie "solite" riflessioni...

Un quiz che ho trovato piuttosto divertente, ma che ho visto essere stato dimostrato in modo un po' troppo laborioso... Tocca a voi!
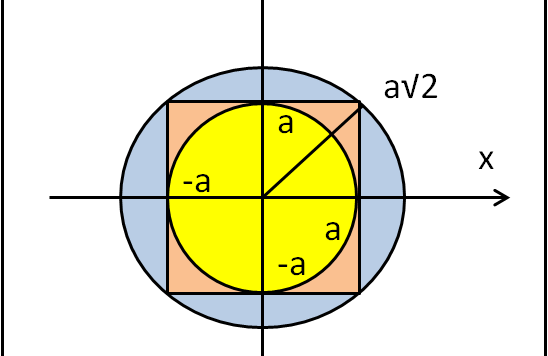
A Gauss piacevano gli integrali doppi e attraverso di essi ha risolto un integrale "semplice" che sembrava impossibile. Un integrale fondamentale nel calcolo statistico dato che si riferisce proprio alla gaussiana, ossia alla distribuzione delle probabilità dei valori che una variabile può assumere. Ad esempio: misurando l'altezza delle persone ci regala l'altezza media e lo scarto relativo a tale valore. In altre parole, non vi è campo della Scienza che non abbia bisogno della distribuzione gaussiana, detta anche "normale".