C'era da aspettarselo... Sembrava troppo semplice la forma di Ultima Thule. Le ultimi immagini (non ancora visibili) sembrano portarci nel fantastico mondo di Flatlandia.
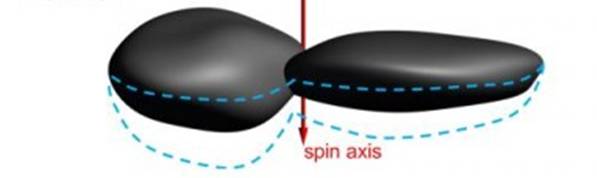

C'era da aspettarselo... Sembrava troppo semplice la forma di Ultima Thule. Le ultimi immagini (non ancora visibili) sembrano portarci nel fantastico mondo di Flatlandia.
Un articolo poco astrofisico e decisamente osservativo, legato essenzialmente a ciò che appare e non a ciò che è. Tuttavia, ci permette di dare qualche informazione non banale e di conoscere il nostro cielo stellato su tempi scala diversi dai soliti.

Li chiamano oggetti Herbig - Haro, ma non sono altro che i primi vagiti (molto potenti) di stelle che stanno nascendo. Per la prima volta ne è stato individuato uno nella luce visibile fuori dalla nostra galassia. Tutti i bambini sono uguali nell'Universo!

Parallelamente agli eventi relativi all'evolversi della vicenda dei diritti umani,
descritti nell'articolo precedente, che avrebbero portato alla dichiarazione del diritto naturale degli uomini alla vita, alla libertà ed alla ricerca della felicità, si sviluppava nel contesto religioso la vicenda della “inquisizione”, istituzione fondata dalla chiesa cattolica nel 1184 allo scopo di indagare e punire, mediante un apposito tribunale, i sostenitori di teorie considerate contrarie alla ortodossia cattolica (le cosiddette eresie).

Sarebbe bello vedere la presenza di molecole organiche e la loro evoluzione in un disco protoplanetario che non sia il nostro. soprattutto se la stella che lo accudisce è decisamente molto giovane, ancora in fase di formazione completa. Basta chiederlo ... e ALMA ve lo fornisce in un piatto d'argento!

Potete cercare di nascondervi in tutti i modi, ma Hubble è un segugio fantastico e vi scoverà ovunque, per quanto astuti voi siate stati.
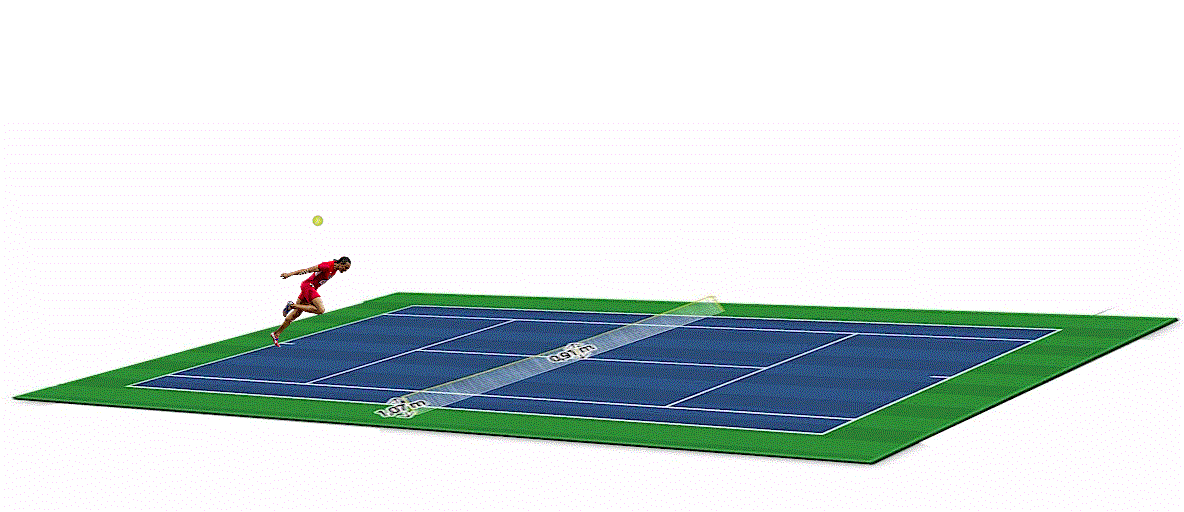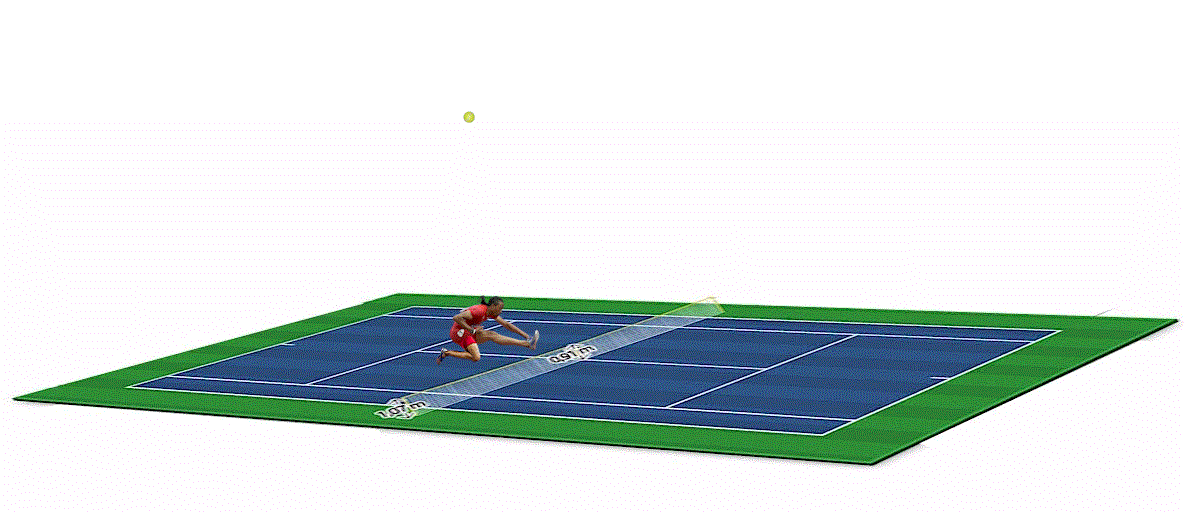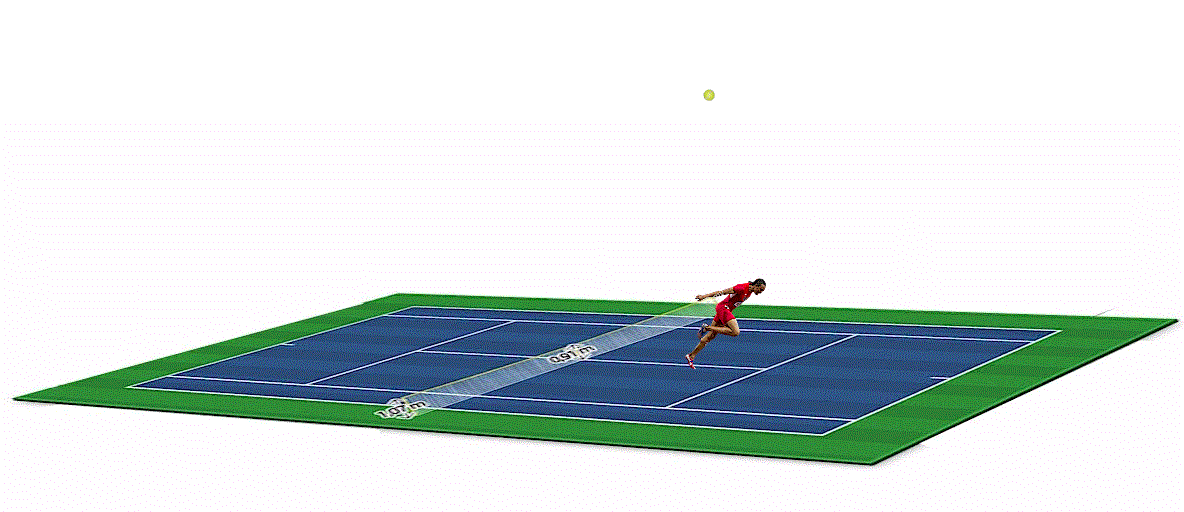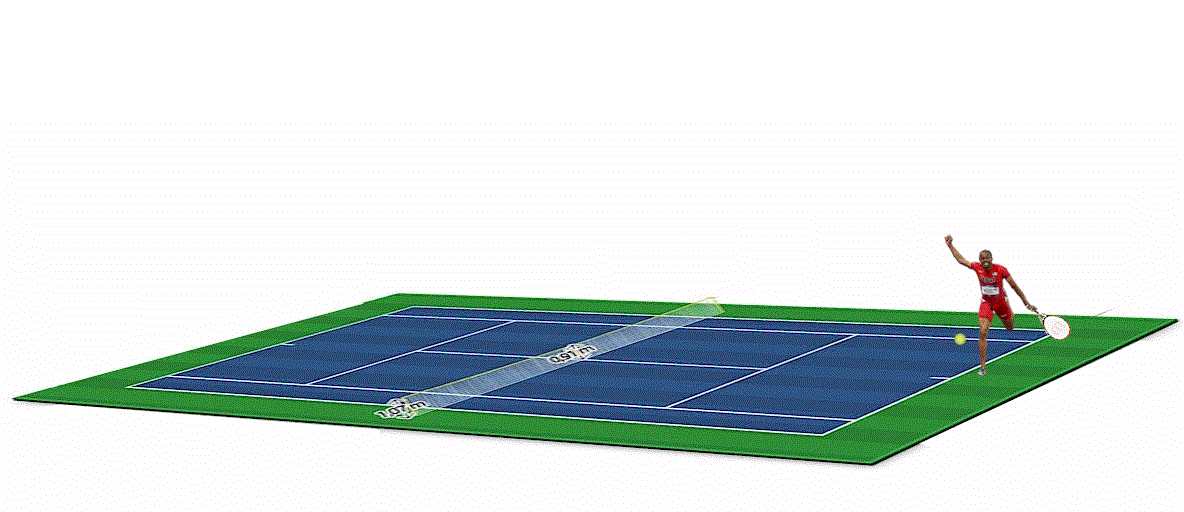
Dopo aver giocato a golf tra mamba e arbitri molto parziali, dedichiamoci a un gioco meno “pericoloso”: il tennis. Ma sarà proprio così?Questo articolo scritto a due teste e quattro mani (quelle di Maurizio e quelle di Vincenzo) nasce da un'idea paranoica di Pautasso in onore del suo grande amico Fantozzi. Chi vuol provare ha tutti i dati a sua disposizione.
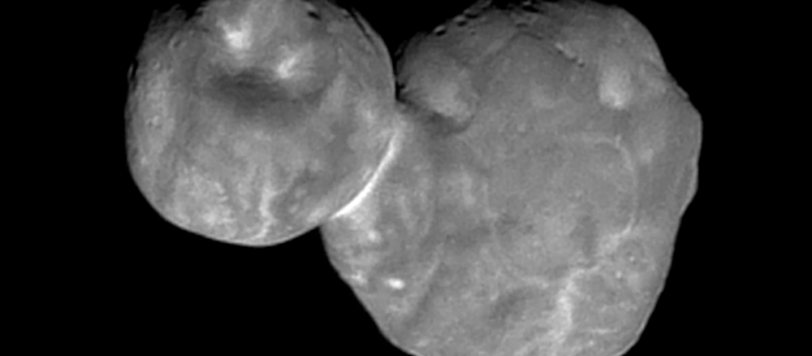
L'ultima immagine di Ultima Thule comincia a dare informazioni molto particolari. Vi propongo una mia personale interpretazione, ben sapendo che non ho certo le possibilità di analisi del team della missione.
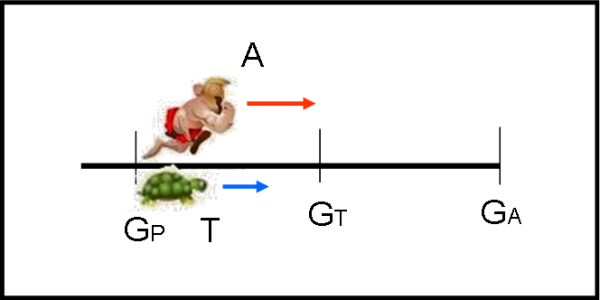
Questo articolo era già apparso, ma il compito dei tre giudici non era stato definito molto bene e ne conseguivano soluzioni ambigue. Ringrazio Guido per avere sollevato il problema. In questa versione credo che i vari compiti siano decisamente ben stabiliti... comunque, se vi sono problemi... parliamone! Con Achille e la tartaruga non si sa mai dove si va a finire...

Un gruppo di astronomi giapponesi ha usato dei telescopi all'altezza di quelli amatoriali (28 cm di diametro) e un'attrezzatura standard, per "vedere" per la prima volta un oggetto della fascia di Kuiper di solo 1.3 km. Davide che sconfigge Golia?

Dedicato a chi vuole farsi una propria idea sulla problematica dei cambiamenti climatici, questo articolo è stato scritto dal nostro amico Fiorentino e mette a confronto uno studio serio sulle cause della sesta estinzione di massa (attualmente in corso) con l’utilizzo fattone da un noto divulgatore.
Dedicato anche al nostro Enzone (che, al momento della pubblicazione, non ne sa niente perché Fiorentino ha voluto fargli una sorpresa), vi offriamo questo fulgido esempio di divulgazione affinché ne traiate stimolo per leggere sempre fonti diverse sullo stesso argomento e... pensare, pensare, pensare!

Una domanda che forse molti si fanno, ma che probabilmente non hanno il coraggio di formulare. I bambini, invece, non si pongono problemi di questo tipo e possono far nascere ricerche non certo banali o inutili.

Un proiettile sparato verso l'alto da un cannone si allontana progressivamente dal centro della Terra. Ad ogni altitudine sarà soggetto a valori di g diversi, dato che l'effetto gravitazionale è inversamente proporzionale al quadrato della distanza. Se quest'ultima aumenta, si avrà un decremento quadratico inverso del valore della gravità rispetto quella a livello del mare che indichiamo con go
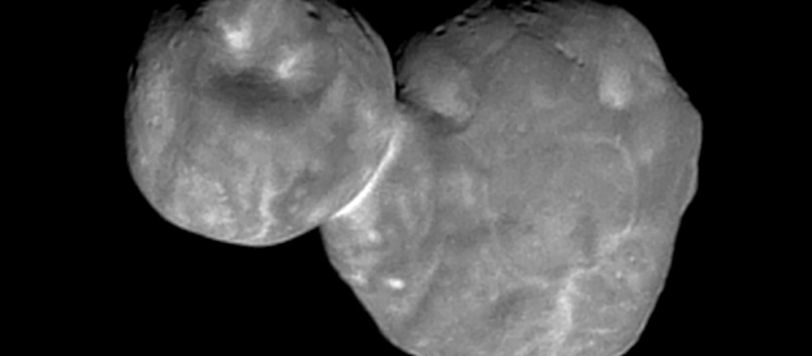
Con la giusta e dovuta calma stanno arrivano le immagini a più alta risoluzione di Ultima Thule. L'ultima arrivata è del primo gennaio, quando la sonda era a 6700 km dall'oggetto celeste, sette minuti prima di raggiungere la minima distanza.

Una delle immagini più celebri riprese dallo Space Telescope c'è sicuramente quella chiamata HUDF (Hubble Ultra-Deep Field) che permette di osservare in un piccolissimo campo (pochi minuti d'arco) oggetti, la cui luce è partita circa fin da 13 miliardi di anni fa. Si stima che vi siano parecchie migliaia di galassie in quella piccolissima zona dell'Universo (così come in qualsiasi altra parte, ovviamente).