Svolgiamo insieme un problema geometrico di cui diamo cinque soluzioni. Magari inizieremo ad amare di più la geometria...
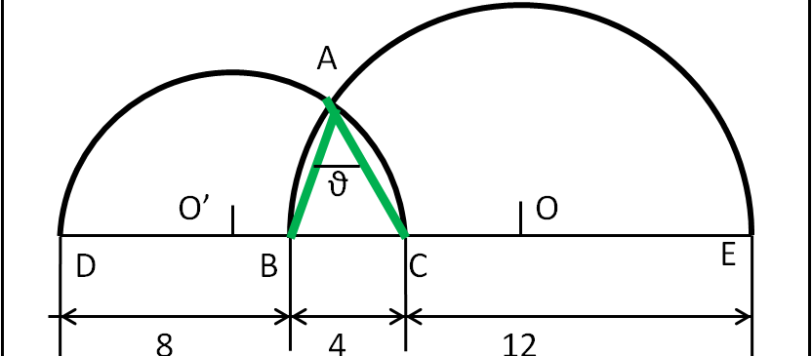

Svolgiamo insieme un problema geometrico di cui diamo cinque soluzioni. Magari inizieremo ad amare di più la geometria...
Un eccezionale esperimento, svoltosi al CERN, ha mostrato che l'antimateria subisce la gravità come la materia.
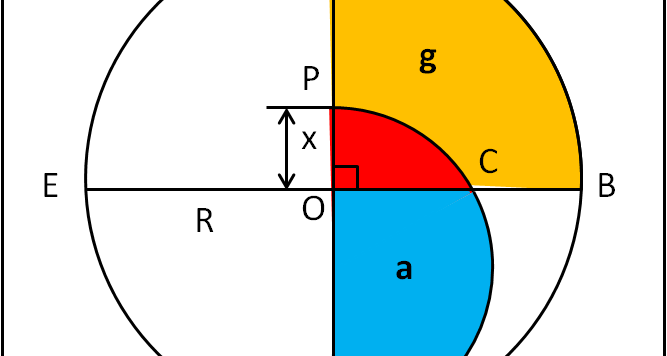
Una soluzione semplicissima a cui ha risposto solo Andy, un super esperto in geometria e non solo.
Mentre su Krull ciascuno ha la propria casa, sulla Terra, dove ci sono nove miliardi di abitanti, capita che una casa appartenga contemporaneamente a più persone. Ciascuno ne possiede una parte, e per far capire a tutti quanta se ne possiede si sono inventati i millesimi, una cosa micidiale.
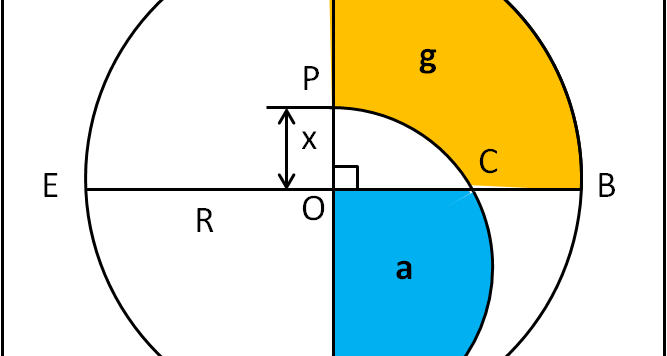
Torno alla mia cara geometria con un quiz estremamente semplice, che abbisogna solo di colpo c'occhio e un briciolo di intuito. Chissà che non si muovano i meno esperti? I calcoli da svolgere sono proprio alla portata di tutti!
Approfittiamo del quiz sull'espressione apparentemente diabolica per introdurre e imparare un'identità dovuta a una grande matematica.

Il telescopio Webb continua a sfornare informazioni sull'Universo giovane e risulta sempre più chiaro che la crescita e l'evoluzione delle galassie è stata molto più rapida di quanto si credesse fino a pochi anni fa.

L'attività del James Webb Space Telescope, dopo il primo anno di osservazioni, sta producendo significativi risultati che iniziano a chiarire le modalità del passaggio tra la Fase Oscura dell'universo ed il termine dell'era della Reionizzazione, confermando l'idea di un universo giovane molto dinamico e già notevolmente differenziato nei suoi elementi costitutivi.
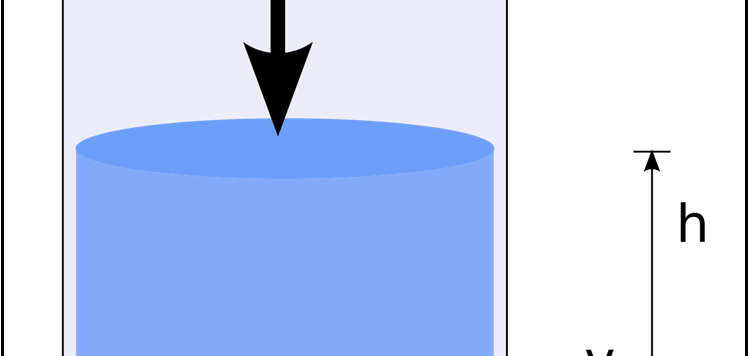
Continuiamo con la cinematica, aggiungendo una formula particolarmente utile per risolvere problemi con moto uniformemente accelerato. Non stupisca se c'è di mezzo Torricelli.
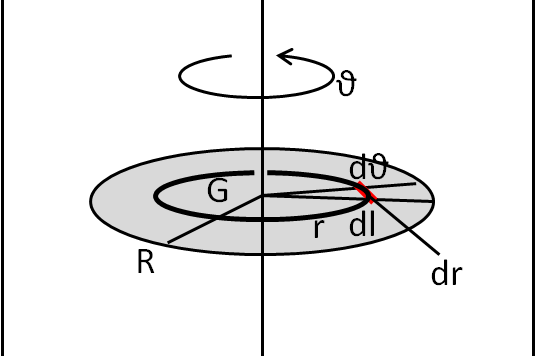
Continuiamo con i nostri momenti d'inerzia. Questa volta tocca all'anello sottile e al disco sottile.
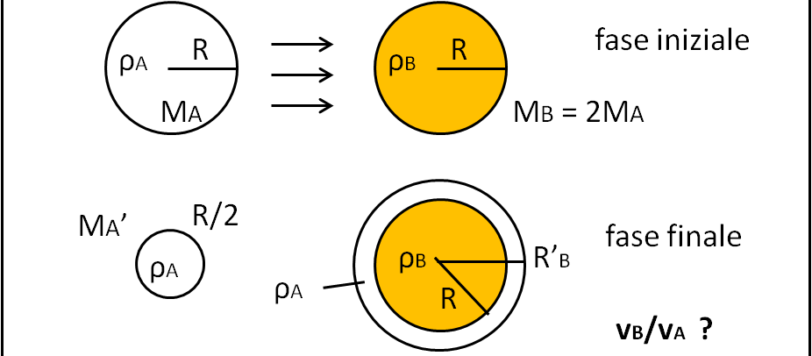
Un problema estratto da uno dei test di ammissione più difficili al mondo. Risolviamolo assieme...
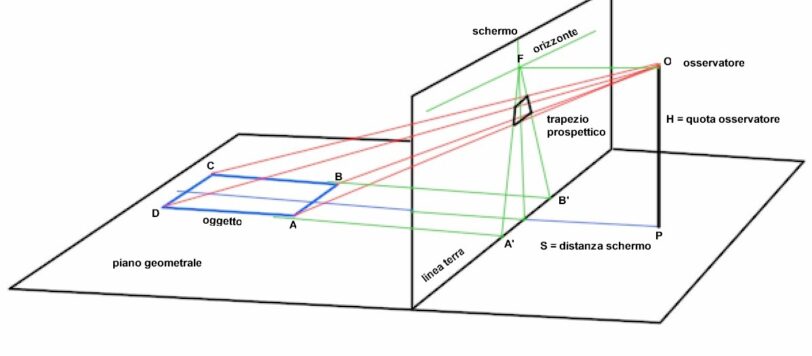
Nel precedente articolo intitolato “il pavone planò e cosa vide?” avevo promesso che avrei ripreso l'argomento utilizzando un quadro prospettico in posizione mobile (a distanza costante dall'osservatore). Questo accorgimento permette di risolvere il problema di rappresentare in prospettiva centrale la visione durante la planata in base a semplici relazioni che legano le variabili.