Beh... forse ho semplificato un po' troppo la situazione, ma il concetto di base è abbastanza corretto e ... realistico. La nostra Daniela-Scherzy non c'è andata così distante...


Beh... forse ho semplificato un po' troppo la situazione, ma il concetto di base è abbastanza corretto e ... realistico. La nostra Daniela-Scherzy non c'è andata così distante...

Cari amici, la generalizzazione del problema iniziale mi ha portato a cercare una nuova strada per descrivere il "fenomeno" geometrico. Una strada che mi è sembrata molto interessante e, all'apparenza almeno, del tutto inesplorata. Il bello è che potrebbe essere resa benissimo da una animazione (vero Arturo?) o permettere di costruire un qualche aggeggio concreto (vero Frank?). Fatemelo dire: possiamo chiamarlo "l'ultimo (ma anche il primo!) teorema di Zappalà o, meglio, di Zappalat" e che Fermat non me ne voglia!

Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.

Il quiz dei due cerchi, "incatenati" al triangolo equilatero, sembra aver perso di interesse. Peccato... perché proprio la seconda parte è quella più interessante, che ci permette addirittura di enunciare un "nuovo" teorema, simile a tanti ricavati dai greci antichi. A quanto mi risulta non mi sembra che sia mai stato enunciato, ma potrei sbagliarmi. Comunque un piccolissimo tassello geometrico in più del nostro circolo.

Non bastava il "nostro" Frank a essere sempre esagerato nei commenti, adesso ci si mettono pure i radiotelescopi! Dopo il miglior giocatore di golf (forse...), ecco anche due radio galassie da primato!

Torna a farci visita il caro amico Fiorentino con una riflessione molto personale e profonda, che costituisce il naturale compimento di quella iniziata col suo originale approccio al "Paradosso Fermi".

Riporto la soluzione della prima parte, ma lascio ancora in sospeso la seconda parte, quella più "giapponese". Il quiz, quindi, continua.

Dobbiamo ammetterlo... i francesi, con la loro boria ormai storica, una cosa meglio di noi la sanno fare realmente: il flan. Un piatto terribile che illude e poi distrugge senza pietà.

In questo articolo propongo alcuni degli argomenti affrontati da Enzo nel 6° articolo della serie “La relatività Generale al microscopio” applicati al caso particolare delle coordinate cartesiane e coordinate polari nello spazio Euclideo. L'obiettivo è di illustrare tramite queste due coordinate il percorso che porta al tensore metrico o metrica.

In questo articolo descrivo la realizzazione di un modello di geometria solida con il quale ho voluto verificare il funzionamento di una montatura equatoriale, ossia un particolare sostegno di un telescopio molto utilizzato in ambito amatoriale e non solo. La montatura equatoriale consente con un unico movimento, manuale o motorizzato, di "inseguire" il moto apparente di un astro nel cielo, in realtà ruotando in sincrono col moto di rotazione terrestre.

Anche il microcosmo ha la sua gerarchia nobiliare... Forse i terrestri ne subiranno gli effetti. Ma se ne accorgeranno?

Ultimamente sfrutto molto le domande dei lettori sia pubbliche che private per affrontare problemi mai toccati o toccati in modo molto superficiale. Me ne è stata fatta una che mi ha stimolato ad addentrarmi, nel modo più semplice possibile, verso una problematica che dire vasta è troppo poco. Soprattutto, non sarà facile mantenere un livello relativamente "basso". Questa domanda, però, mi ha istigato a proporne una a voi che ci serva un po' come antipasto...

Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.
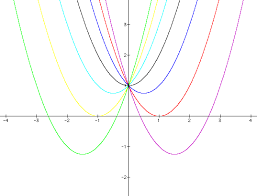
In realtà, risolvere un'equazione di secondo grado non è difficile. L'unico problema può essere, per qualcuno, ricordare a memoria la formula risolutiva. Ma è veramente necessario? Rifacendosi in parte ai babilonesi, possiamo dire di NO.

E' un periodo che sforno tanti quiz e sono contento di vedere che riscuotono successo. Anzi, mi accorgo che, a volte uno a volte un altro, siete prontissimi a rispondere. Voglio provare a divertirmi anch'io, sicuro della vostra partecipazione!