Un quiz che ha ottenuto un enorme successo, ma anche risultati altalenanti. La difficoltà stava nell'accorgersi di una terza via di accesso, mascherata dalla visione tridimensionale.


Un quiz che ha ottenuto un enorme successo, ma anche risultati altalenanti. La difficoltà stava nell'accorgersi di una terza via di accesso, mascherata dalla visione tridimensionale.

Perfette le soluzioni grafiche e discorsive di Fabry e Paolo. Vale la pena, comunque, scrivere la soluzione con qualche figura.

No, non è la cometa di Natale e posso anche dirvi che è stata osservabile solo per pochi minuti (poco più di due). Come può essere successo? Beh... proprio in pieno giorno può succedere qualcosa di veramente affascinante!

Ebbene sì... ho già pubblicato questo racconto molte volte, ma ho intenzione di riproporlo ogni anno in occasione del Natale. Qualcuno tra i lettori più affezionati conosce già il motivo di tale insistenza, gli altri lo capiranno leggendo l'introduzione e la postfazione.
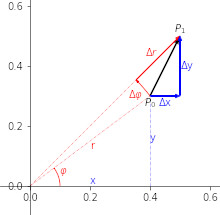
In questo articolo propongo alcune domande ed alcuni approfondimenti sulle trasformazioni dei vettori trattate nell'articolo La Relatività Generale al microscopio. 4: I Tensori **. Cerco anche di collegare i vettori e le loro trasformazioni con le entità trattate negli articoli precedenti. In particolare scalari (tensori di rango 0) e gradienti.

Un simpatico problemino di geometria euclidea. Decisamente facile, ma vediamo chi trova il sistema più rapido ed elegante per dare la giusta risposta...

Riproponiamo, suddividendola in alcune puntate, la nostra analisi del pensiero e delle opere di Giordano Bruno, ovvero colui che possiamo considerare il vero iniziatore dell'astrofisica e della cosmologia moderna.
Fu, infatti, questo piccolo monaco (ma solo di statura), quando Galileo ancora era poco più che un bambino, a frantumare le "granitiche" sfere di cristallo aristoteliche con la sola forza del pensiero, riuscendo a volare là dove nessun altro arriverà per oltre tre secoli dopo di lui.
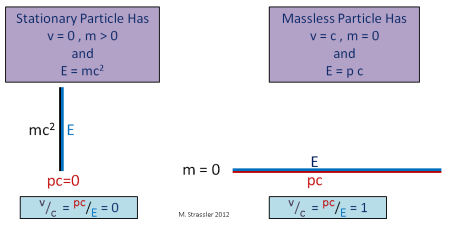
Un piccolo appunto di dinamica relativistica per rispondere coralmente a una domanda che mi è stata fatta varie volte. Ne abbiamo già parlato, ma non è mai ripetitivo ribadire i concetti essenziali della relatività

Una notizia che ci potevamo, ovviamente, aspettare. La tecnologia osservativa di oggi permette senza dubbio di trovare oggetti già "costruiti" (come le galassie primordiali), che si avvicinino sempre di più al limite dell'Universo Osservabile. Niente di sensazionale, ma un'occasione in più per richiamare i concetti fondamentali di ciò che ci mostra l'Universo.
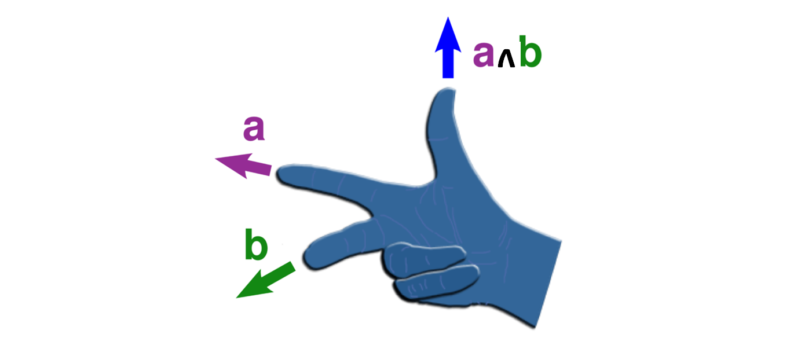
Introduciamo nuovamente i tensori, tenendo ben presente che abbiamo lavorato tanto per riuscire a manipolare correttamente le loro coordinate, cambiando sistema di riferimento. Ci aspetta un bel ... "lavoro"!

Riproponiamo, diviso in sei puntate, un articolo che deve rappresentare l'ABC per chi volge lo sguardo al cielo: una semplice spiegazione di come funziona quella stupefacente macchina del tempo che l'Universo mette a disposizione di chiunque abbia occhi e testa (e un pizzico di buona volontà!) per comprenderla ed ammirarla. In questa quinta puntata iniziamo ad affrontare il problema della distanza tra due oggetti cosmici.

Diamo una versione molto semplificata, e anche un po' ironica, di un effetto verificato da studi continui e approfonditi effettuati sull'Oceano Artico. Una piccola rivoluzione...
Il mio solito sfogo giornaliero... abbiate pazienza, ma lo uso come valvola di scarico. Nessuno è, ovviamente, obbligato a leggerli.

Grazie ad un pianeta molto "discolo", riprende vigore la speranza di poter individuare il nostro nono pianeta.
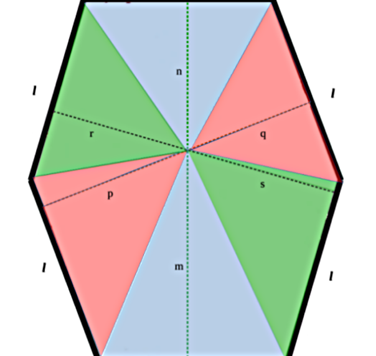
Il nostro caro amico Andy, solutore più che abile di molti quiz proposti, ha voluto analizzare con maggiori dettagli il problema dell'esagono con i lati uguali e paralleli a due a due, ma con gli angoli ai vertici diversi tra loro. Così facendo ha trovato risultati più compatti, utilizzando altre formule relative alle aree. Pensiamo che valga la pena proporvele, dato che sono un ghiotto boccone per chi ama la geometria. Un grazie di cuore ad Andy!