La soluzione è decisamente più semplice di quello che poteva apparire alla prima occhiata. Basta far ruotare un triangolo e il gioco è fatto.
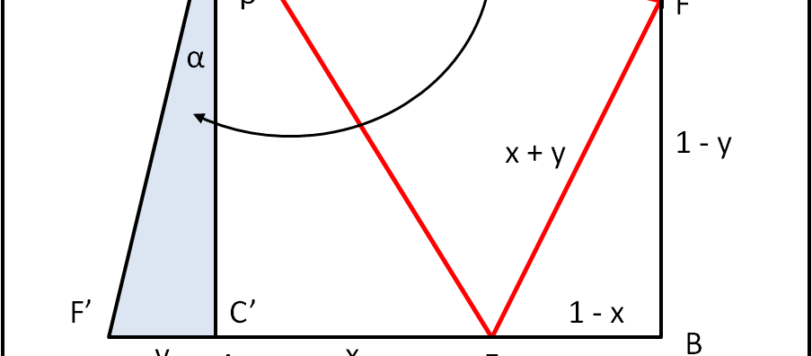

La soluzione è decisamente più semplice di quello che poteva apparire alla prima occhiata. Basta far ruotare un triangolo e il gioco è fatto.

Un buco nero super massiccio ha perso la sua "corona" e immediatamente essa è apparsa sotto forma di virus nel nostro piccolo mondo, dominato -a parole- da una creatura poco rispettosa nei confronti del Cosmo. Un altro degli scherzi di cui è capace l'Universo? Forse sì... e -magari- ce lo meritiamo.

Prendiamo in mano le nostre equazioni parametriche generali e cominciamo a vederne dei casi particolari. Ritroveremo quelle che già abbiamo trattato la volta scorsa, ma anche molte, molte altre... Potete costruirvele da soli o fare un programmino allo scopo.

Il quiz sul distanziamento sociale è stato risolto brillantemente dai "nostri" abilissimi lettori. Non mi resta che sintetizzare il tutto e proporre una dimostrazione facile (va beh... "abbastanza" facile) per la geniale formula di Binet.

So che papà (Enzo) ha già riportato una rapida descrizione del viaggio, ma - a sua insaputa- ho voluto esprimere anche le mie impressioni a riguardo. Un viaggio molto importante per noi, in questo momento, ed è giusto che sia raccontato anche da me (Barbara alias Bucci alias Bucciriccia...).

Cadiamo quasi nella fantascienza, ma... in fondo, in fondo, non sarebbe poi una cosa così strana e potrebbe spiegare molte cose, perfino la materia oscura.

Lo sappiamo bene: più le stelle sono massicce e meno vivono, ma la loro trasformazione finale è più che plateale, dando origine alle supernove, uno dei fenomeni più luminosi ed energetici dell'Universo. Questa è la norma, ma si pensava che questi veri giganti del Cosmo potessero anche "andarsene" in silenzio, senza far "rumore"... Forse è stata osservata la prima stella veramente discreta.

Questo è un blog di astrofisica e, come tale, vuole raccontare la bellezza e la perfezione dell'Universo. Molto spesso (sempre più spesso) ci dimentichiamo di farne parte e manifestiamo comportamenti e pensieri che ci scagliano proprio all'opposto, nell'ignoranza e nella futilità più becera. Ma non è sempre stato così e la storia antica ce lo insegna. Per cui non penso di andare fuori tema ricordando di cosa è stato capace l'homo sapiens, prima di diventare homo smartphonicus. In pratica, brevi appunti di viaggio tra cultura, bellezza, armonia e capacità di pensare con la propria testa.
"La spiegazione del moto del gatto parmi assai semplice. Questo animale abbandonato a sé, descrive colla sua coda un cerchio nel piano perpendicolare all'asse del suo corpo. In conseguenza, pel principio delle aree, il resto del suo corpo deve rotare in senso opposto al moto della coda; e quando ha rotato della quantità voluta, egli ferma la sua coda e con ciò arresta contemporaneamente il moto suo rotatorio, salvando in tal guisa sé ed il principio delle aree" (Giuseppe Peano)

Prima di parlare di una ricerca che potrebbe essere fondamentale, voglio ricordare con grande affetto chi l'ha portata avanti: Mariateresa Crosta dell'Osservatorio di Torino. Ragazza estremamente capace, simpatica e intelligente, in cerca di un posto, ha lottato con la calma di chi è sicuro dei proprio mezzi e c'è riuscita. Oggi, inoltre, potrebbe avere smontato del tutto il comodo castello di carte su cui si basa la materia oscura. Un "brava!" a lei e un bravo anche a Mario, guida della missione Gaia.
Cari amici, sono tornato a casa dopo una decina di giorni di "vacanza" in Toscana e nel Lazio. Pochi giorni e spero di riprendere il ritmo... Qualche appunto di viaggio. Dopo aver visto la grandezza, lo splendore, l'abilità architettonica e la perfetta organizzazione pubblica di una città portuale e commerciale come Ostia Antica (più di […]

Una carrellata di vecchi articoli per scoprire o riscoprire il gigante buono (?) del sistema solare...

Non vi è dubbio che il transito di Venere davanti al Sole sia un fenomeno tra i più seguiti da qualsiasi tipo di "osservatori" del Cielo. Si sente parlare di cicli di visibilità che spesso permettono di vedere il fenomeno dopo pochi anni e a volte dopo più di un secolo. Si trovano dappertutto numeri e date ad essi relativi, ma forse poco si fa per spiegare come tutto ciò avviene. Questo articolo non vi dà, perciò, i soliti “numeri”, ma descrive soltanto i concetti base. Poi tutto diventa semplice...
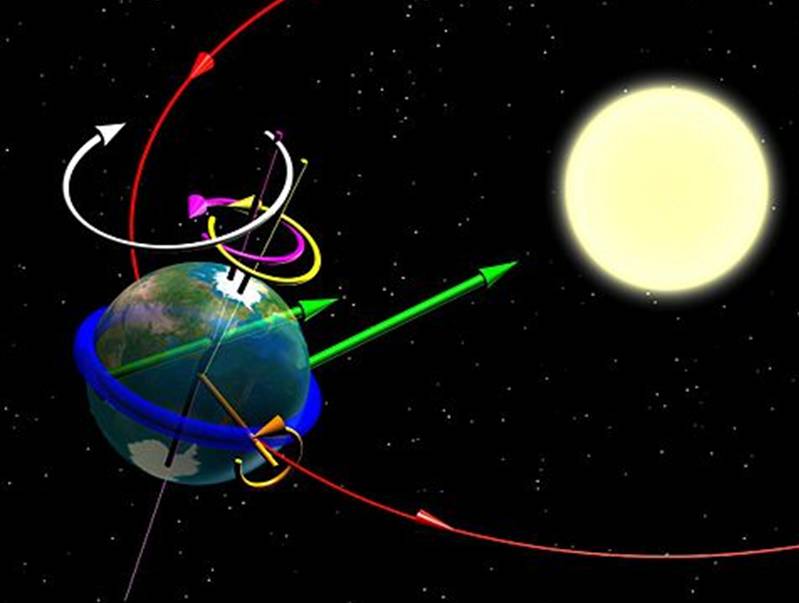
Tutti avranno sentito parlare di precessione almeno una volta. Essa viene citata sia quando di parla di spostamento della stella polare come indicatrice della direzione del polo nord sia quando si discute sul cambiamento delle costellazioni dello zodiaco sia, a volte, delle coordinate delle stelle. In qualche modo si parla di precessione solo per i suoi effetti, ma non riguardo alla sua vera ragione fisica. Eppure, la osserviamo sempre quando facciamo girare una trottola e i telescopi spaziali non potrebbero puntare esattamente gli oggetti celesti senza "trottole" molto speciali.