Il titolo è alquanto sibillino, ma vuol dire, in pratica, che se ci accorgiamo che la Natura rompe quella che noi consideravamo una perfetta simmetria, è molto facile che il modello da noi costruito sia sbagliato.

Il titolo è alquanto sibillino, ma vuol dire, in pratica, che se ci accorgiamo che la Natura rompe quella che noi consideravamo una perfetta simmetria, è molto facile che il modello da noi costruito sia sbagliato.

Ogni promessa è un debito; questa appendice vuole giustificare (con il metodo rigoroso dell'analisi) le equazioni differenziali comparse nello studio dei modelli SIS e SI. Mi dispiace, dovevo farlo prima.
Come detto, questa serie di articoli vuole essere veramente divulgativa e adatta a qualsiasi livello, sempre che si abbia già un'infarinatura dei concetti di limite, derivata e integrale. Per ottenere ciò, penso che non mi picchierete se a volte sarò ripetitivo e quasi banale. Nella versione definitiva, si potrà sempre cercare di compattare meglio la materia e renderla più uniforme. Per adesso pensiamo ad affrontare nel modo più chiaro possibile i concetti fondamentali.

Ed ecco finalmente il quarto amico, il più schivo e il meno conosciuto, che segue, però, come un ombra gli altri tre. La sua conoscenza ci permette di fare amicizia con una trasformazione nel piano, più semplice sicuramente della geometria inversiva: l'omotetia.

Le leggi dell'Universo funzionano molto bene e perché allora non utilizzarle a qualsiasi scala?
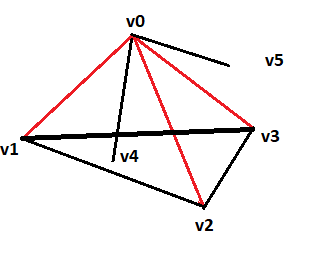
Il quiz lo trovate qui. Sostanzialmente, mi sembra che Maurizio abbia imbroccato la soluzione, anche se con la sua metodologia empirico-intuitiva che secondo me lo contraddistingue. Vi dò una soluzione un po' più formale al quiz, semplice e concisa. Ho aggiunto due figure per capirci meglio , Scusate per la loro rozzezza. La domanda era questa: […]

Con questo articolo torniamo a uno degli scopi base del nostro Circolo: quello di rendere comprensibili a tutti coloro che hanno la volontà di conoscere, le meraviglie dell'Universo e, di conseguenza, della fisica e del suo linguaggio (la matematica). Tratteremo in modo elementare le equazioni differenziali, cardine di tutta la ricerca scientifica, non solo astronomica. Inizieremo dalle più semplici, quelle che hanno un riscontro immediato nella realtà di tutti i giorni, e poi, un po' alla volta e valutando la vostra risposta, allargheremo sempre più il discorso.

Questo articolo costituisce il seguito all'articolo REALTÀ E RAPPRESENTAZIONE : I MODELLI MATEMATICI. NON è necessaria alcuna conoscenza delle equazioni differenziali, ma solo del concetto di derivata , e dell'integrale di 1/x , assieme alla derivata del logaritmo. Il termine equazione differenziale può spaventare; ma non è altro che una equazione dove compare una funzione incognita assieme alla sua derivata. Quindi niente di trascendentale.D'altronde , ormai la scuola superiore fornisce questi concetti sia agli istituti commerciali che a quelli professionali ; basta un po' di buona volontà per la comprensione dei calcoli che purtroppo sono alla base dei modelli. Dopo aver trattato il modello SI, tratteremo ora il modello SIS. Ma vediamo cos'è..

Vedo che i quattro amici non hanno riscontrato grande interesse... Poco male, dato che lo scopo del quiz era quello di introdurre una delle tante scoperte di Eulero uno dei più grandi matematici della storia, già noto attraverso la matematica superiore di Umberto e per la più bella formula matematica in assoluto (come diceva il grande Feynman). Noi tratteremo il tutto in modo estremamente elementare.

ALMA, malgrado il periodo poco favorevole alla ricerca sul campo, non perdona e ci regala un tassello importantissimo sulla relazione, probabilmente abbastanza burrascosa, tra buchi neri galattici e formazione stellare.
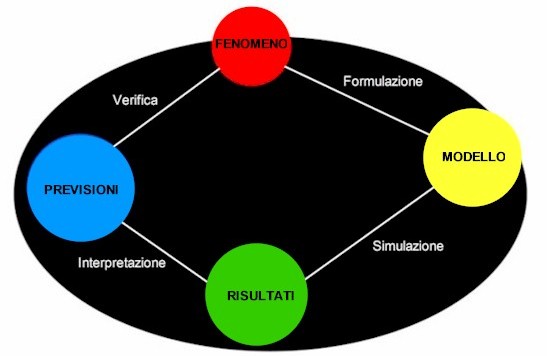
Può la matematica predire il futuro? Ecco un esempio di Realtà e rappresentazione , un modello matematico deterministico.

Quattro amici molto legati tra loro. Chi mai saranno? Come al solito, i più esperti aspettino almeno 48 ore prima di parlare...
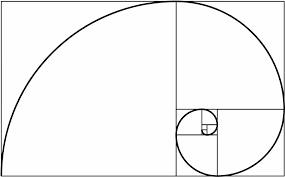
Le prodezze del Teorema di Tolomeo proseguono, aiutandoci a dimostrare facilmente una proprietà poco conosciuta collegata ai triangoli equilateri e a finire in bocca alla sezione aurea. Con questo articolo finiamo la nostra piccola-lunga storia sul Teorema di Tolomeo, ma non è detto che non ci si ritorni su, prima o poi.
Cari tutti, per colpa mia che ho pensato di mettere in campo anche il problema enorme che sta colpendo la povera, ignorante e piccola umanità messa sotto scacco da un banalissimo virus, siamo finiti in un ginepraio che ha preso tutte le sembianze di facebook o social analoghi. Ho pensato (sbagliando sicuramente, ma me ne […]