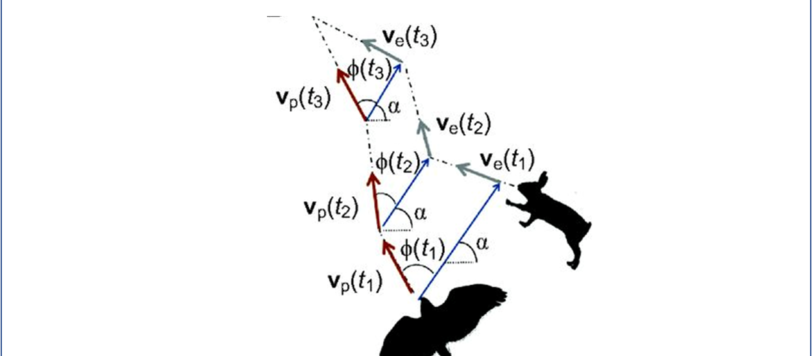
Nessuno ha dato una risposta... pazienza. Il vero scopo del quiz era, comunque, duplice. Innanzitutto avvicinarsi a una strategia realmente seguita da alcuni animali per la loro caccia e, poi, cercare di definire nel modo migliore un gioco da tavola basato su questa strategia. Forza, siamo appena all'inizio. I lauti guadagni saranno equamente divisi...
Nella vorticosa fucina del blog, ogni tanto succede che si producano contemporaneamente articoli gemelli, del resto anche nel mondo dei numeri esistono i “primi gemelli” e tutti ne hanno profondo rispetto. L'ultimo di questi casi riguarda la metamorfosi della catenaria in parabola, evento che è sotto i nostri occhi ogni volta che osserviamo un ponte sospeso.
Affrontiamo lo scoglio maggiore di questa serie di articoli, ossia determiniamo l'equazione della catenaria, quella "strana" condizione di equilibrio di una catenella sospesa tra due chiodi intorno alla quale Galileo ha disquisito, accorgendosi di non essere in grado di ricavarla e accontentandosi di approssimarla a una parabola.
Ve ne eravate dimenticati? Sicuramente no... ma per un po' di tempo il perfido Dott. Nobody aveva lasciato in pace il nostro povero Pippo, come promessogli. Tuttavia, quando si è Nobody, ogni promessa NON viene mantenuta. Questa volta sembra che per Pippo la faccenda diventi molto difficile. Un problema che ci immerge (con tutte le cautele del caso) nell'ambiguità tra onda e particella. Insomma, un quiz, per così dire, quantistico.
Affrontiamo un'altro semplice problema, veramente "pratico", facendoci aiutare da una nuova equazione differenziale. Si ringrazia il prezioso contributo di Oreste Pautasso che, spero, abbia imparato quanto siano utili le nostre equazioni.
In questo lungo articolo affrontiamo di petto il problema della carta igienica, limitando gli approcci a un numero abbastanza ristretto (se ne potrebbero tentare anche altri). Come vedremo potrebbe sembrare un problema del tutto inutile e ridicolo, ma –in fondo- oltre che a metterci di fronte a una matematica di livello crescente (e quindi molto utile per verificare le proprie conoscenze) ci può far riflettere su problematiche ben più ampie e fondamentali. Inoltre, lo reputiamo abbastanza divertente! L’articolo, iniziato da Vincenzo, ha visto la fattiva collaborazione di Daniela e Maurizio, oltre che i commenti puntuali di Umberto e Leandro. Un lavoro veramente corale che può essere letto da tutti, cosa questa che auspichiamo fortemente.
Quanto è lungo un rotolo di carta igienica?
Parlare di barche, navi e della loro stabilità sia con mare calmo che agitato comporterebbe un intero libro (e magari nemmeno basterebbe). Tuttavia, dato che, comunque, una nave galleggia per effetto del Teorema di Archimede non possiamo esimerci dal dare qualche informazione di base a riguardo.
Approfondiamo l'argomento della stabilità dell'equilibrio che abbiamo trattato parlando del galleggiamento nell'ambito del teorema (o "principio") di Archimede, riproponendo un articolo che qualche anno fa abbiamo proposto sotto forma di quiz.
Il titolo è alquanto sibillino, ma vuol dire, in pratica, che se ci accorgiamo che la Natura rompe quella che noi consideravamo una perfetta simmetria, è molto facile che il modello da noi costruito sia sbagliato.
Come detto, questa serie di articoli vuole essere veramente divulgativa e adatta a qualsiasi livello, sempre che si abbia già un'infarinatura dei concetti di limite, derivata e integrale. Per ottenere ciò, penso che non mi picchierete se a volte sarò ripetitivo e quasi banale. Nella versione definitiva, si potrà sempre cercare di compattare meglio la materia e renderla più uniforme. Per adesso pensiamo ad affrontare nel modo più chiaro possibile i concetti fondamentali.
Con questo articolo torniamo a uno degli scopi base del nostro Circolo: quello di rendere comprensibili a tutti coloro che hanno la volontà di conoscere, le meraviglie dell'Universo e, di conseguenza, della fisica e del suo linguaggio (la matematica). Tratteremo in modo elementare le equazioni differenziali, cardine di tutta la ricerca scientifica, non solo astronomica. Inizieremo dalle più semplici, quelle che hanno un riscontro immediato nella realtà di tutti i giorni, e poi, un po' alla volta e valutando la vostra risposta, allargheremo sempre più il discorso.
Dopo la discussione sulle densità, siamo pronti ad affrontare la parte più interessante legata alla spinta di Archimede, ossia il galleggiamento. D'altra parte se si riescono ad attraversare gli oceani con una nave è fondamentale che la nave non vada a fondo! Non perdetevi questo articolo, dato che -forse- scoprirete un fenomeno poco conosciuto, che può dare il via a varie simulazioni "casalinghe".
Tra le quattro interazioni (o forze) della Natura quella meno "visibile", ma forse più utile perché esista la materia, è quella nucleare forte. Una forza che si è dimostrata capace di adattarsi a condizioni critiche.
La volta precedente abbiamo capito il significato della spinta di Archimede e perché deve entrare in ballo il peso del liquido spostato. Ora possiamo tranquillamente arrivare scrivere la formula che lega il peso effettivo del corpo immerso e la spinta di Archimede.
In questo articolo cercherò di unire, come si suol dire, l'utile al dilettevole. L'argomento è quello dei satelliti geostazionari. Come noto, questi sono satelliti posti in orbita equatoriale attorno alla Terra ad una quota tale che essi, pur muovendosi rispetto ad un osservatore solidale con un sistema di riferimento posto nello spazio, risultano fermi in […]