Cari amici, che ne dite di un bel viaggetto fino a un buco nero? Magari proprio su Cygnus X-1 a 8000 Anni Luce da noi? E, se tutto va bene, cercare anche, in seguito, di entrare al suo interno?
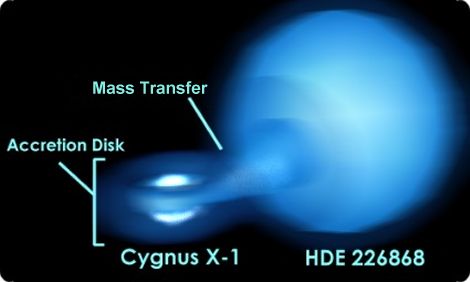

Cari amici, che ne dite di un bel viaggetto fino a un buco nero? Magari proprio su Cygnus X-1 a 8000 Anni Luce da noi? E, se tutto va bene, cercare anche, in seguito, di entrare al suo interno?
Le risposte avute finora sono sicuramente “abbastanza” (a parte qualche incertezza sulle altezze) precise, ma sono anche un po’ troppo “elevate”. Bastava qualcosa di molto più empirico, ma sufficiente a Peppa per disegnare con buona precisione ciò che viene richiesto da Pappo e Pippo
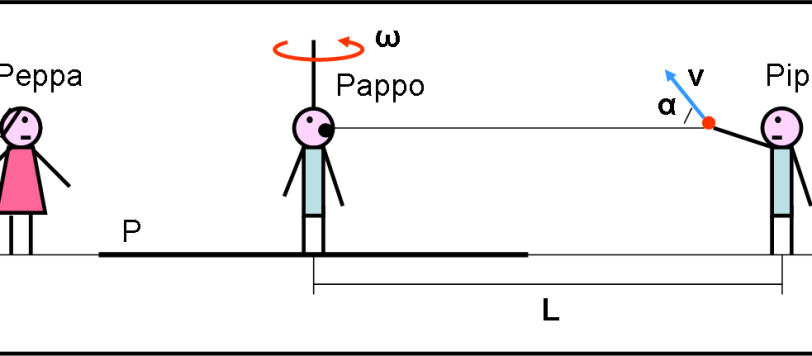
Pappo e Pippo a furia di mangiar torte si sono “beccati” una terribile gastroenterite. Conclusione? Mai più dolci per loro e per il dopo pranzo solo e soltanto frutta. Ovviamente, due menti vulcaniche come le loro hanno subito escogitato un gioco fuori dal normale per rimanere nei limiti della dieta impostagli dal medico.

Abbiamo già visto come l’Universo e i suoi attori siano capaci di realizzare opere d’arte strabilianti, che non temono certo il confronto con quelle create dal genio umano, anzi. Basterebbe dire che anche noi siamo Universo e tutto potrebbe risolversi facilmente. Tuttavia, il Cosmo è limitato nelle sue esibizioni artistiche, dato che può mostrarcele solo attraverso l’informazione luminosa. Sì, sappiamo che sta nascendo anche la trasmissione tramite onde gravitazionali, ma siamo ancora all’asilo infantile e i veri capolavori non possono essere recepiti dai nostri mezzi troppo elementari. Tuttavia, le onde gravitazionali ci lanciano verso un discorso ben più ampio che ho piacere di condividere con voi, in attesa di una qualche nuova rivoluzione scientifica.
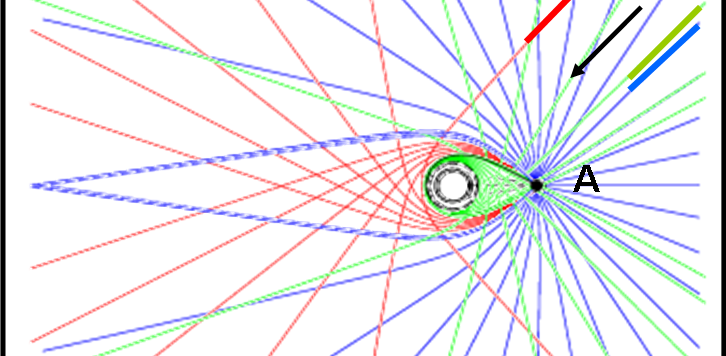
Potrebbero bastare le immagini… ma esse meritano di essere spiegate un po’ meglio. Oltretutto, dobbiamo anche dare una risposta al quiz sulla densità e la gravità (risolto brillantemente). Si notano facilmente cose abbastanza strane, ma molte altre, ugualmente interessanti, sono decisamente meno visibili. Andiamo, soprattutto, incontro a molte deformazioni subite dai raggi luminosi e l’idea che essi siano quanto di più rettilineo esista in Natura,è solo un lontano ricordo. La colpa di tutto ciò è sempre e soltanto della teoria della relatività di Einstein che ha permesso la scoperta di questi oggetti, che rappresentano il confine tra realtà e assurdità.

Questo lungo articolo copre tutti gli aspetti (o quasi) dell'aberrazione luminosa. Un fenomeno di interesse estremo sia consideratolo attraverso la fisica classica che attraverso la relatività, di cui è una semplice approssimazione. Come si vede gli asterischi sono variabili, da due a quattro, a seconda della trattazione che si utilizza, Sta al lettore decidere se seguire il tutto o saltare gli argomenti più ostici. Per questi ultimi è necessaria una preparazione di base della relatività ristretta e della sua rappresentazione nel diagramma di Minkowski. Per gli altri basta solo un minimo di attenzione e di volontà di capire. In ogni modo, entrambe le strade portano a una conclusione che reputo soddisfacente.

Un piccolo quiz che anticipa la seconda parte del viaggio verso un buco nero stellare. Tanto per tastare il polso…
Con questo racconto concludiamo (almeno per ora) il fedele resoconto sulla origine delle unità di misura. I personaggi che vedremo in azione sono piuttosto turbolenti e non sarà facile tenerli a bada tutti in una volta, comunque....
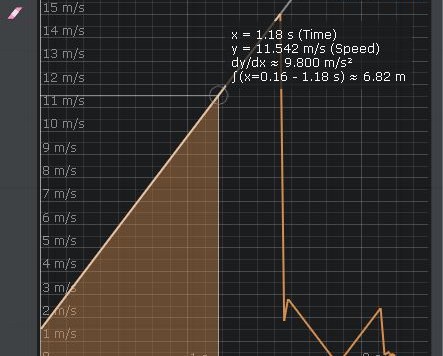
Grazie a tutti coloro che hanno manifestato interesse per questo quiz, attestato dall'elevato numero di visite, e a coloro che hanno partecipato con le proprie risposte. La risposta alla domanda posta dal quiz è affermativa. L'occorrente per far cadere più lentamente il disco cilindrico è già tutto presente e non ci serve altro. Basta solo […]

Proseguiamo il nostro viaggio nella vera storia delle unità di misura con la ricostruzione di quali siano state le reali motivazioni che hanno condotto Michael Faraday a concepire il Farad.
Se non fosse stata definita l'unità di misura di questa grandezza, ci sarebbe una gran confusione nell'utilizzo dei condensatori, componenti essenziali per una sterminata quantità di apparecchiature senza le quali la nostra vita sarebbe diversa.

Finalmente un nuovo viaggio nello spazio per i nostri piccoli e sempre più avventurosi amici! Questa volta, tuttavia, non si limiteranno a qualche giro intorno alla Terra, bensì affronteranno lo spazio profondo, con tutti i suoi pericoli, tutte le sue opportunità, ma, soprattutto, tutte le informazioni che ci dà!
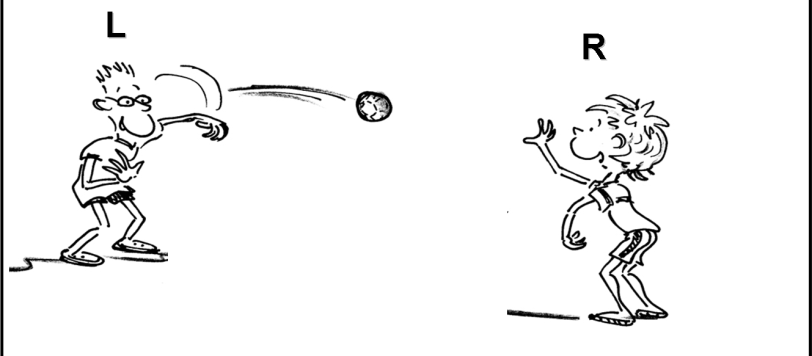
Tempo fa, mentre facevo una passeggiata alla ricerca di un’ispirazione per un nuovo articoletto divulgativo da pubblicare nel nostro Circolo, la mia attenzione venne catturata da due ragazzini che stavano giocando a lanciarsi una pallina da tennis e da un distinto signore che li osservava con aria divertita e interessata… stavo per andarmene, quando mi accorsi che il signore stava usando un cronometro, quindi mi resi conto che in realtà quello non era un semplice gioco, ma un vero e proprio esperimento scientifico… potevo non fermarmi a curiosare?

Dopo diversi quiz di matematica, ve ne proponiamo stavolta uno di fisica, abbastanza vicino all'esperienza quotidiana.
Prosegue, con questa seconda puntata, l'avventura di Oreste Pautasso nel mondo degli analemmi...

Dopo l'Ampere e l'Ohm, siamo giunti al terzo episodio di questa ricostruzione della verità sulla genesi di alcune delle più note unità di misura. E' la volta del Coulomb, l'unità storica della carica elettrica.
Inizia, con questo racconto, una incursione nel mondo delle meridiane, che vi darà la risposta alla domanda che mai avete osato fare: cosa è mai quella specie di otto che campeggia sotto lo stilo in corrispondenza della linea del mezzogiorno? Forse la firma del pittore che ha disegnato il quadrante? Oppure una raffigurazione magica il cui significato è andato perduto? Serve forse a qualche scopo pratico? Quali sono i criteri con cui viene tracciato?
Ebbene, se avrete un po' di pazienza e non vi perderete questa e le prossime puntate, avrete tutte le risposte a questi interrogativi