Proseguiamo con il calcolo dei momenti d'inerzia di solidi particolari.
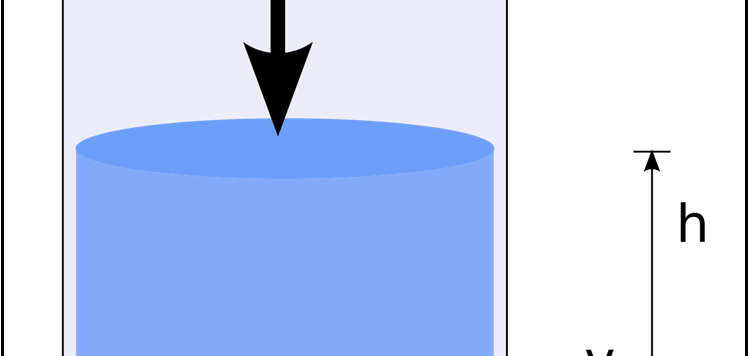
Continuiamo con la cinematica, aggiungendo una formula particolarmente utile per risolvere problemi con moto uniformemente accelerato. Non stupisca se c'è di mezzo Torricelli.
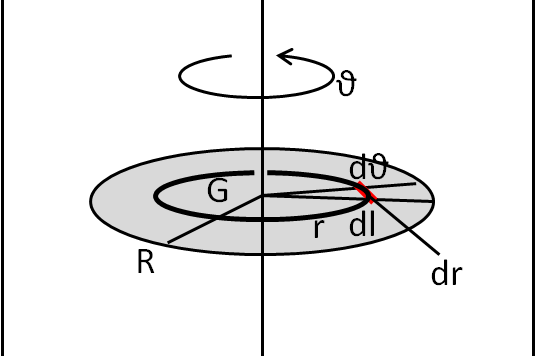
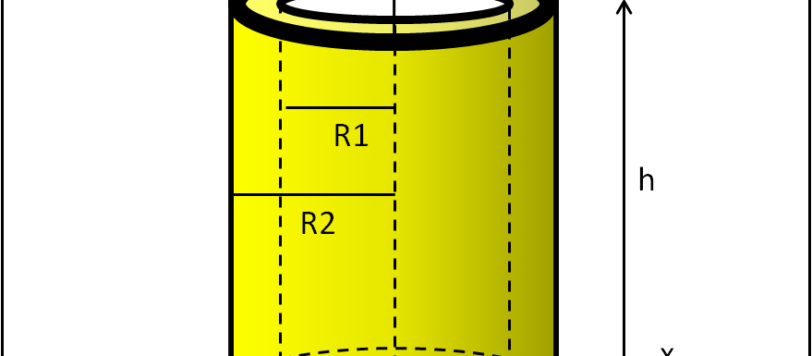
Continuiamo con i nostri momenti d'inerzia. Questa volta tocca all'anello sottile e al disco sottile.
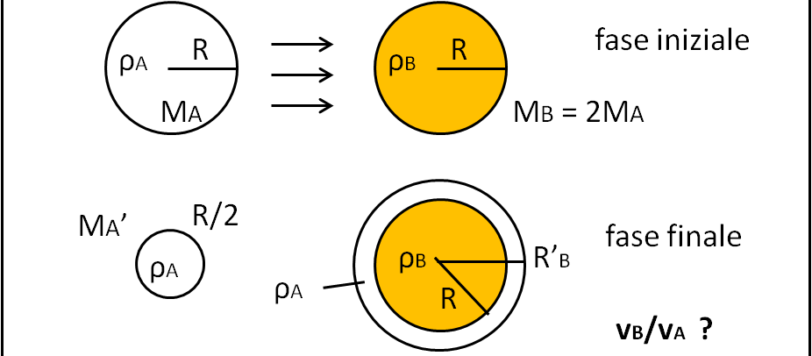
Un problema estratto da uno dei test di ammissione più difficili al mondo. Risolviamolo assieme...
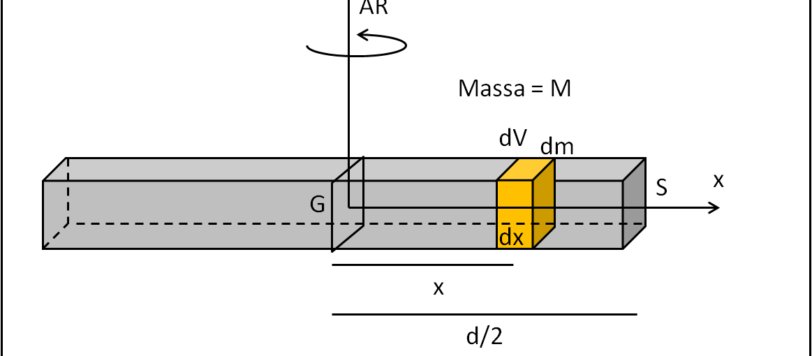
Negli svariati articoli di fisica classica, abbiamo sempre trascurato un po' il momento d'inerzia, ossia la "reazione" di un corpo a qualcosa che vuole farlo ruotare. Qualcosa, perciò, che è l'equivalente della massa in un moto traslatorio. Analizziamo da vicino e vediamo di calcolare i momenti d'inerzia di alcuni corpi rigidi con forme differenti. Iniziamo con una barretta di ferro...
Proseguendo nell'esecuzione di semplici esercizi di cinematica è meglio tener conto di possibili errori nell'applicazione delle formule fondamentali della cinematica.

Anche se intento a preparare semplici esercizi di cinematica e , in generale, di fisica classica, non potevo lasciare inoperosi i più esperti siano essi silenziosi oppure no. Chiamiamolo pure ... un anticipo di inverno!

Ricominciamo da... tre. Occupiamoci un po' della fisica classica e, in particolare, della meccanica, iniziando col ricavare le formule base della cinematica e risolvendo un primo esercizio.
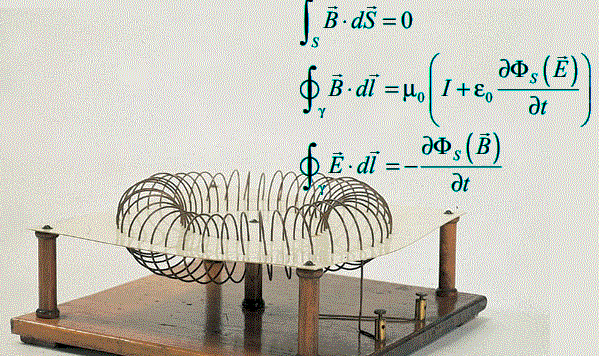
La più grande realizzazione di Maxwell fu, nel 1864, l’unificazione delle forze elettrica e magnetica, creando, con le celebri equazioni differenziali che portano il suo nome, il rigoroso modello di riferimento in cui inquadrare le osservazioni di Faraday.
Si trattava di un evento fondamentale, le cui conseguenze investirono il futuro di tutta la fisica.
La forma di queste equazioni ha guidato scienziati come Lorentz, Poincaré e Einstein alle trasformazioni spaziotemporali della relatività speciale che, a loro volta hanno condotto alla concezione di spaziotempo di Minkowski.

In quel secolo e mezzo o poco più che separa Newton da Einstein, molti personaggi scrivono importanti pagine nel libro della Scienza ma, tra di essi, ce n’è uno che, più degli altri, può essere considerato un vero e proprio ponte tra quei due geni assoluti, risolvendo il dubbio di Newton e ponendo le basi per le intuizioni di Einstein: nacque a Londra nel 1791, morì nel 1867, diventò il più grande fisico sperimentale dei suoi tempi e di lui bisognerebbe parlare di più.

Semplifichiamo di molto un argomento piuttosto complesso che permette ai paracadutisti e agli acrobati del cielo di lanciarsi con relativa tranquillità.

Se c’è una cosa sulla quale difficilmente nutriamo dubbi è la natura solida, liquida o gassosa di un determinato materiale.
Invece qualche dubbio dovremmo averlo...
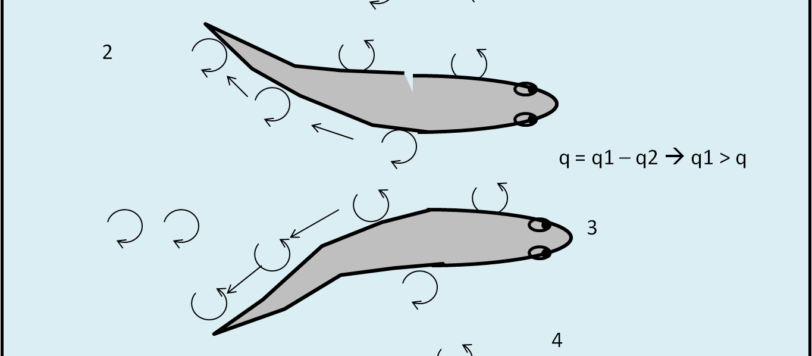
I pesci non hanno braccia come i nuotatori; i pesci non hanno un motore come i sottomarini; eppure nuotano perfettamente in linea retta a velocità impensabili. Come fanno?

Una soluzione tecnologica di estrema semplicità ha permesso di far correre i treni su due stretti binari senza farli deragliare, soprattutto in curva. Vediamo di descriverla in modo puramente geometrico.
In attesa che il prof. riprenda a scrivere nuovi articoli, continuiamo a riproporre alcune delle "chicche" che abbiamo gelosamente conservato nell'archivio universale del blog!

Che i gatti cadono sempre in piedi, lo sappiamo tutti!
Quello che, invece, non tutti sappiamo è quanto la spiegazione di questo apparente paradosso fisico abbia impegnato la comunità scientifica. Basti pensare che la prima ipotesi (sbagliata) è stata formulata nel '700 e che, ancora oggi, qualche margine di dubbio permane...