Un'altra ciliegina nata durante uno scambio di commenti con Alberto parlando di effetto fionda. La faccenda si era risolta, ma penso non sia male trasformarla in uno dei saporiti frutti sotto spirito...
Cari amici, la generalizzazione del problema iniziale mi ha portato a cercare una nuova strada per descrivere il "fenomeno" geometrico. Una strada che mi è sembrata molto interessante e, all'apparenza almeno, del tutto inesplorata. Il bello è che potrebbe essere resa benissimo da una animazione (vero Arturo?) o permettere di costruire un qualche aggeggio concreto (vero Frank?). Fatemelo dire: possiamo chiamarlo "l'ultimo (ma anche il primo!) teorema di Zappalà o, meglio, di Zappalat" e che Fermat non me ne voglia!
L'ipotesi della natura corpuscolare della luce si fa solitamente risalire a Newton. Ma non è così! Basterebbe avere meno "campanilismo" scientifico...
Siamo a un passo dalla catastrofe nucleare e l'orologio del presidente si è rotto! Come fare?
Doveva essere una news, molto breve, è invece è diventato un articolo dai molti risvolti. Una scoperta veramente importante che ha avuto una scarsa eco, se non nei rispettivi campi scientifici. Un vero peccato e ho cercato di inserire il maggior numero di informazioni (a modo mio, ovviamente). Non l'ho voluto spezzare in due o più parti, proprio per creare quell'unità multidisciplinare che domina il tutto. Ci sarebbe comunque da parlarne ancora di più; è un po' come le noccioline: una tira l'altra!
Volete scegliere il percorso più breve per salvare un uomo in mare prima che sia aggredito da uno squalo? Una formica vi chiede come raggiungere velocemente un certo punto di un barattolo? Oppure desiderate minimizzare il rischio di incontrare un ostacolo posto sulla vostra strada da un perfido professore (Nobody o Zappalà, chi lo sa...)?
Niente paura! La soluzione a questi e ad altri problemi è a portata di mano...
Phileas Fogg l'aveva fatto in 80 giorni (ricordate Giulio Verne?). Bene, i tempi cambiano e oggi Phileas Fogg scommetterebbe di farlo in solo 6 ore!
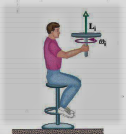
La conservazione del momento angolare è un fenomeno che tutti conosciamo in quanto è proprio quello che fa girare sempre più veloce una pattinatrice sul ghiaccio, se avvicina le braccia al corpo. E’ lo stesso fenomeno che fa girare le stelle di neutroni come trottole impazzite. Ma i suoi giochi sono molteplici, analizziamone uno...
Un bel cartoncino, una bilancia ultra precisa e possiamo far meglio di Archimede!
Da sempre l'umanità è ossessionata dalla costruzione di automi: macchine che si muovono e si comportanto come essere viventi. Ma cosa c'entrano i nostri amici gatti?
Prima di passare a cose più serie divertiamoci un po' con la scatola di Galton, in qualche modo l'antenato del ben più noto "flipper".
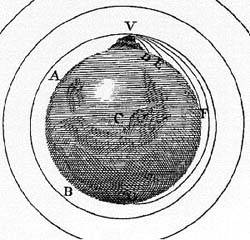
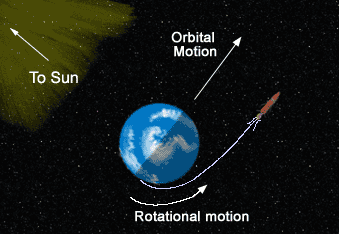
Il linguaggio usato da Galileo per descrivere la caduta dei gravi o il moto di un grave al quale è stata impartita una certa velocità è diverso dal linguaggio usato da Newton per descrivere la "sua" forza di gravità? Sì oppure no? Discutiamone giocando con proiettili, missili intercontinentali e sonde spaziali.
Un simpatico fenomeno di fisica classica (facilmente riproducibile "praticamente") che porta a un risultato a prima vista sorprendente... Oltretutto, ci permette di ricordare alcune grandezze fondamentali e le loro relazioni. I due asterischi valgono per chi conosce già le basi della meccanica, altrimenti è meglio andarle a studiare nell'archivio... o nel libro "La Fisica Addormentata nel Bosco".
Non so a cosa sia dovuto il silenzio totale, ma sicuramente è un quiz con risposta estremamente facile. Che poi io abbia cercato di renderlo apparentemente complicato, fa parte del gioco...
Mettiamo insieme: un paese uscito sconfitto da un conflitto mondiale, un trattato di pace che gli proibisce di costruire armamenti tradizionali, un piccolo gruppo di ragazzi appassionati di razzi e... complice il fatto che i razzi non rientrano tra gli armamenti proibiti (ma solo perché all'epoca del trattato non erano conosciuti), prende il via una serie di eventi che prima genera tanta morte e distruzione, dopodiché porta l'uomo a camminare sulla Luna.
La trama di un nuovo film di fantascienza? No, una storia vera che conosciamo tutti.... ma cosa c'entrano i gatti?
Beh... inseriamo un quiz semplice (anche se non lo sembra del tutto). Buon divertimento!