Sembrava un asteroide, ma oggi ...

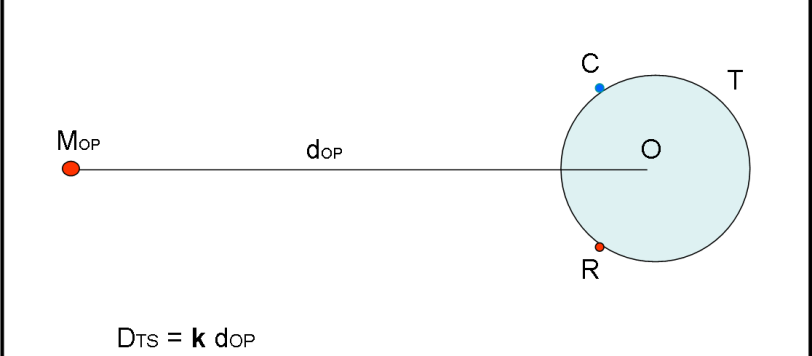
Prima di continuare con la nostra storia della distanza della Terra dal Sole, mettiamoci alla prova con un problemino risolto nel 1672 e quindi di estrema facilità per noi. Tuttavia, vogliamo usare solo ciò che avevano a disposizione a quei tempi. Non andate a cercare nel web dato che troverete sicuramente una parte della risposta, ma, forse, non tutta… Pensateci, quindi, da soli.
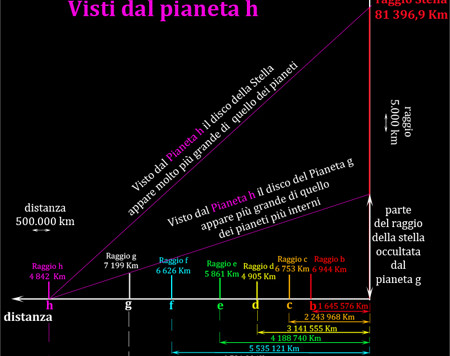
Su Papalla sono un po' preoccupati che solo un terricolo ha risposto ad una delle tre domande del quiz... prima hanno pensato ad un problema di comunicazione... poi hanno pensato che i terricoli forse assomigliano agli abitanti del pianeta timido, meglio noti come i timidoni...
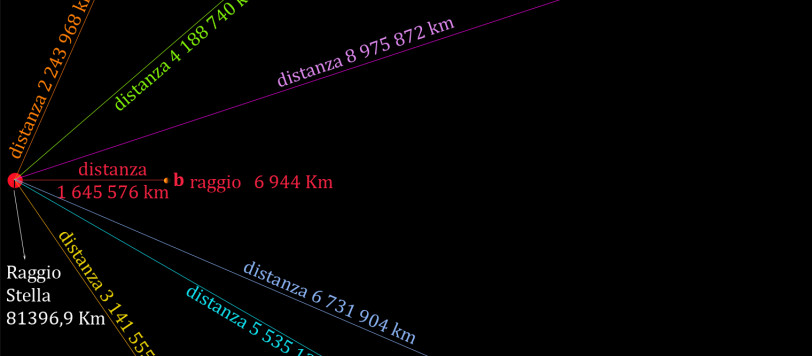
La scoperta dei sette pianeti sette attorno alla nana rossa Trappist-1, ha già mostrato che carta e matita sono più che sufficienti per rappresentare possibili panorami visti dai vari pianeti.
Affidare il compito a qualche software può apparire come la cosa più semplice, ma senza conoscere come quei risultati sono stati ricavati si finisce per dover prendere per vero anche ciò che potrebbe essere frutto di un errore del programma o della sua impostazione...

Seguendo gli articoli di Enzo ho notato che citava l'utilizzo della "lagrangiana", per la soluzione di un problema relativo ai punti lagrangiani. Avevo già visto citato questo misterioso oggetto anche da altri che ne parlavano come di una cosa fondamentale nella fisica classica e, ancora di più, nella fisica moderna. A grandi linee sapevo di cosa si trattasse, ma non avevo mai approfondito l'argomento. La citazione di Enzo mi ha incuriosito ulteriormente e ho cercato di capire meglio cosa fosse questa lagrangiana. Questo articolo raccoglie tutti i capitoli usciti a puntate ed è stato inserito negli approfondimenti.

Su Papalla è giunta voce che i terricoli hanno individuato un sistema planetario che ruota intorno ad una piccola stellina, affettuosamente soprannominata la nana rossa trappista... e i papalli hanno subito provato a realizzare alcune rappresentazione panoramiche...

Nelle precedenti puntate abbiamo fatto conoscenza con alcuni esempi di lagrangiana e visto all'opera l'equazione di Eulero-Lagrange su uno di questi esempi. Ora abbiamo tutti gli elementi per tornare al punto di partenza. La frase di Enzo nell'articolo sui punti lagrangiani che mi aveva inizialmente incuriosito: "Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana". Ma prima dovremo passare per un esempio di applicazione del metodo di Lagrange ad un sistema non inerziale che finora non abbiamo visto. Ci farà incontrare una vecchia amica che ci inizierà a svelare la frase di Enzo.
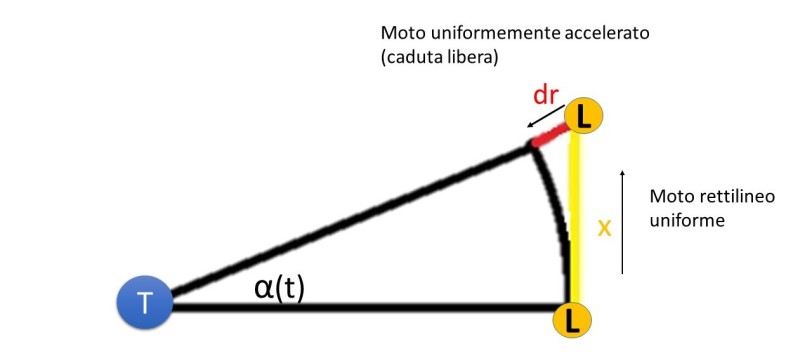
Che sia vera o meno la storia della mela che, dopo aver colpito la testa di Newton, lo avrebbe stimolato ad elaborare la sua Legge di Gravitazione Universale, resta il fatto che nel 1666 intuì che la legge fisica che fa cadere i gravi sulla Terra è la stessa che tiene in orbita la Luna. Ma una cosa è avere un’intuizione, per quanto geniale, altra è riuscire a dimostrarla. Vediamo come ha fatto!
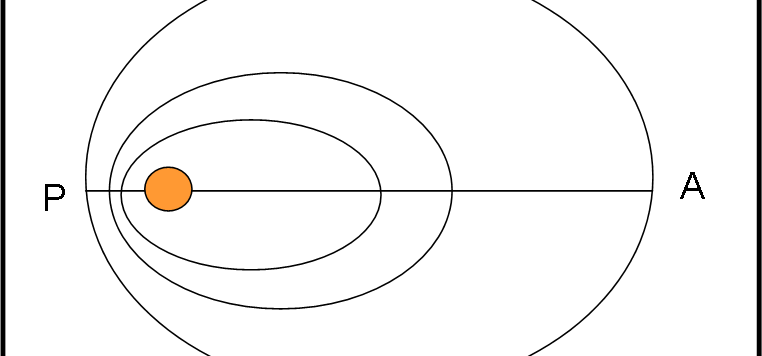
Non esiste soltanto la precessione degli equinozi, quella dovuta alla rotazione dell’asse di rotazione della Terra attorno all’asse perpendicolare all’eclittica. Esistono due altri moti di precessione che si riferiscono alla linea degli apsidi (congiungente perielio-afelio) e alla linea dei nodi (intersezione tra il piano orbitale di un pianeta e quello del Sole). Questi fenomeni non sono solo legati al sistema solare, ma a tutti i sistemi planetari e non solo.
Allineamento planetario: gioia e dolore di molti astrofili. In realtà, spesso e volentieri si fa molta confusione riguardo all’allineamento dei pianeti. Soprattutto, quando lo si vuole riferire a episodi catastrofici di tipo gravitazionale o mareale. Questo articolo cerca di descrivere i vari tipi di allineamento e i metodi per la loro previsione.

In questo articolo, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti.
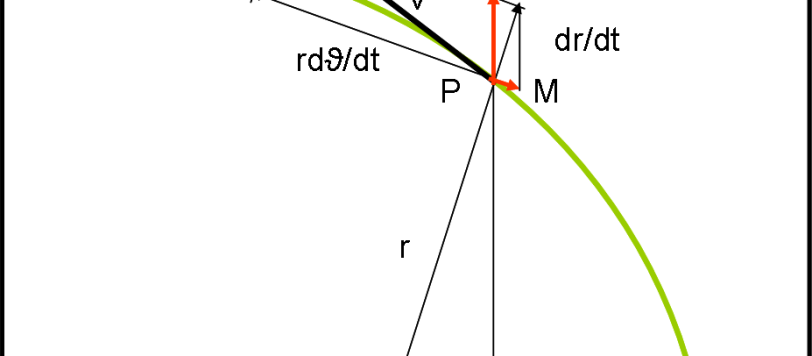
Questo articolo è dedicato alla velocità orbitale di un oggetto nel caso generale dell’ellisse. Lo lascio un po’ in evidenza e poi lo vado a inserire negli approfondimenti, come appendice del moto dei due corpi, di cui utilizza varie relazioni. I richiami che troviamo nel testo si riferiscono a quell’articolo.
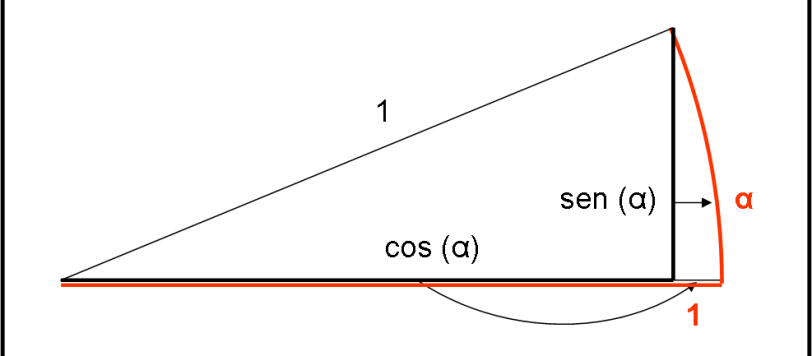
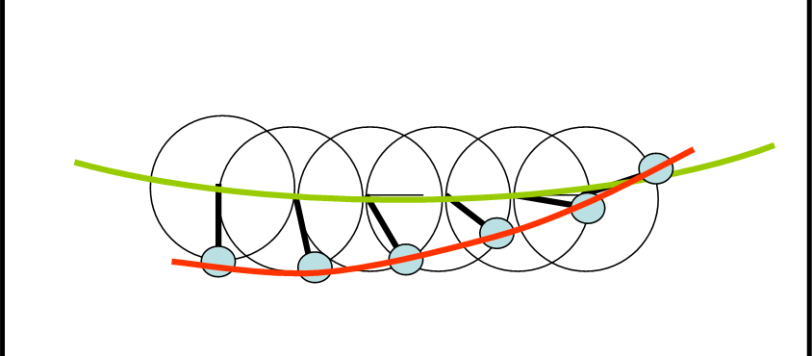
Proponiamo un metodo “antico”, ma sempre utile, per risolvere l’Equazione di Keplero. Lavoreremo per approssimazioni successive, cercando di arrivare al risultato finale (o almeno avvicinarlo il più possibile) attraverso un processo ripetitivo. Come al solito, vi prego di non “snobbare” questo articolo. Non fatelo per me, ma per Keplero…
Questo quiz era passato nel dimenticatoio e grazie a Daniela è tornato alla memoria (mia per prima…). Ne diamo la soluzione che è veramente semplice e che vede la Luna come “rompiscatole” di turno.
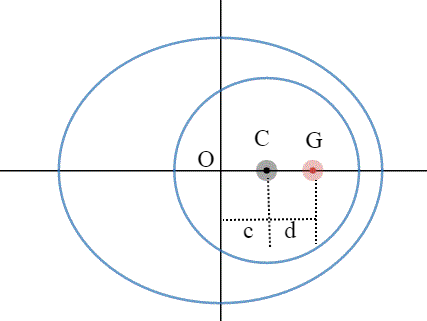
Questo articolo porta il nome del solo Umberto, ma, in realtà è stato elaborato completamente da Fabrizio e da Umberto che hanno ottenuto, indipendentemente, la stessa soluzione. Enzo ha solo aggiunto qualche pezzetto come collante. Una piccola sorpresa nell'ellissi di minimo periodo, ma un esercizio di sicuro valore. Grazie quindi, a nome di tutti, A FABRIZIO e UMBERTO, veri artefici dell'opera d'arte!
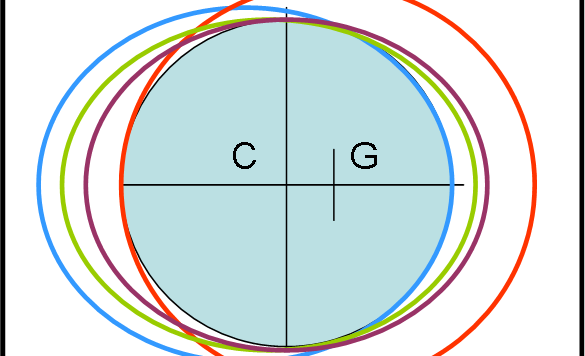
Cari amici, è con vero piacere che devo ammettere di essere caduto, relativamente al quiz sul satellite della Papalterra , in uno di quegli errori di cui avevamo parlato nel famoso QUIZ della formica sul barattolo. Ho considerato un caso limite come soluzione minima senza tener conto di tutta una serie di possibilità. Devo dire grazie a Paolo, Umberto e Fabrizio per avermi messo con le spalle al muro. Questo è il bello di questo Circolo, dove chiunque può sbagliare e tutto serve per continuare a imparare e mettersi alla prova, con allegria e umiltà.