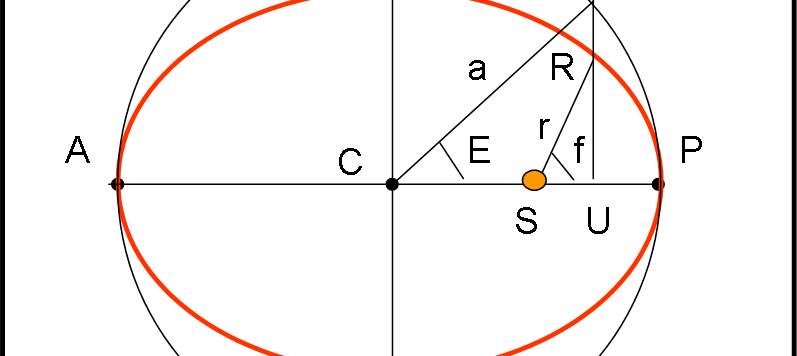
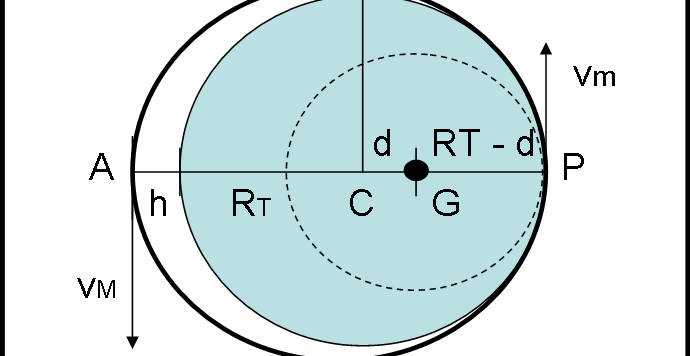
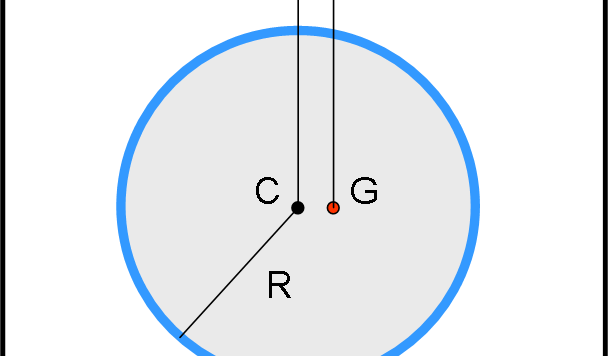
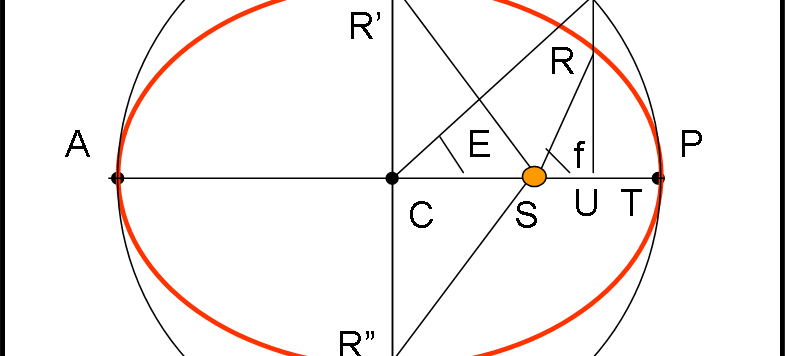
Continuiamo, seguendo Keplero, verso la sua equazione fondamentale che lega anomalia eccentrica e anomalia media. Un'equazione fondamentale che può, però, risolversi solo per approssimazioni successive, un processo, oggi, ridicolo per i calcolatori elettronici. Pensiamo, però, a Keplero che non li aveva ancora...