Ebbene sì, voglio provarci, semplificando il tutto e attribuendogli solo un asterisco. I più esperti non mi guardino male, dato che bisogna pure incominciare...
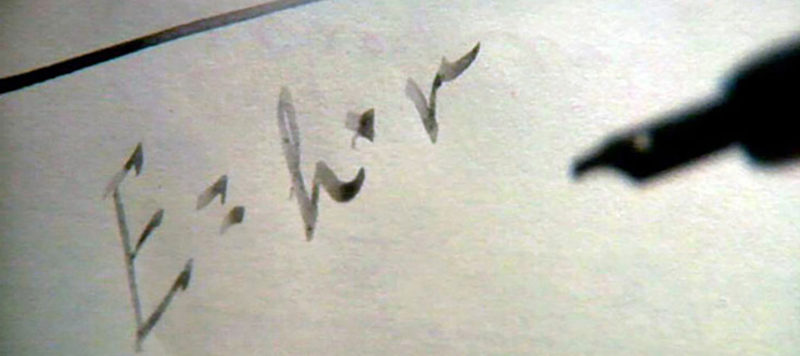
Ho il grande piacere di proporvi un interessantissimo articolo estratto dall'intrigante blog dell'amico Fabio Marzocca. Riguarda il linguaggio, un argomento che stiamo trattando da un po' di tempo. Insomma, cade proprio come il cacio sui maccheroni. Grazie Fabio!
Nella soluzione che propongo a questo quiz ci si rifà pari pari alla formula trovata da Dirac, sia sostituendo pi greco al numero 2 sia scrivendo 2 in altro modo... Ringrazio ufficialmente Karl, Andy e Fabrizio per la volontà, l'interesse e le capacità dimostrate!
Questa volta voglio accontentare i più bravi ed ecco un bel quiz matematico con quattro asterischi che possono anche diventare sei per i bravissimi (e molto fantasiosi).
In questa ultima parte esamineremo il possibile contenuto di una qualsiasi ipotetica teoria locale che rinuncia all'inquietante azione a distanza. Questo esame ci permetterà di delimitare i possibili valori che la grandezza S può avere applicando una teoria locale. L'espressione di questa delimitazione è proprio la disuguaglianza di Bell. Vedremo che i valori che abbiamo ottenuto per S applicando l'interpretazione standard, in alcuni casi non sono compatibili con quelli ottenibili da una qualsiasi ipotetica teoria locale. I risultati sperimentali che hanno indagato questi casi in gran parte non sono nei limiti indicati dalla disuguaglianza di Bell. Quindi, una teoria che vuole prevedere correttamente questi risultati non può fare a meno di quell'inquitante azione a distanza che Einstein aveva evidenziato.
In questo articolo proseguiamo l'analisi delle previsioni della interpretazione standard sui risultati delle misure su una coppia di fotoni in stato entangled. Ricaveremo il valore numerico secondo l'interpretazione standard della grandezza utilizzata da Bell nella sua disuguaglianza. Il calcolo verrà fatto analizzando la correlazione tra i risultati delle misure sui due fotoni.
La disuguaglianza di Bell alla quale vogliamo arrivare riguarda un grandezza ricavabile da misure su coppie di fotoni in stato entangled. Partiremo dalla configurazione di apparti che permette di effettuare queste misure. Arriveremo alle espressioni che l'interpretazione standard dà alle probabilità di ciascuno dei possibili risultati di queste misure.
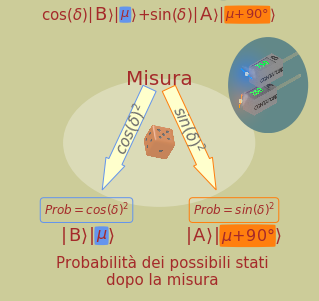
In questo articolo iniziamo ad esplorare come la teoria standard interpreta i fatti che abbiamo visto nei due articoli precedenti. Vedremo come è rappresentato lo stato quantistico di un fotone con la sua polarizzazione e come questo stato evolve al passaggio in un cristallo polarizzatore. Passeremo poi alla descrizione di come il vettore di stato si modifica nel processo di misura (riduzione o collasso del vettore di stato).
Da qualsiasi esperienza, da qualsiasi conoscenza, si può trarre qualche insegnamento filosofico. La MQ non fa eccezione e anzi, offre svariati spunti, utili soprattutto perché in grado di cambiare completamente il nostro modo di vedere le cose. Ecco due tra quelli che secondo me sono i punti salienti.
Proseguo con le descrizione di alcuni fatti sperimentali. L'obiettivo è arrivare alla relazione che lega la polarizzazione dei fotoni entranti in un cristallo polarizzatore con le frazioni di fotoni rivelati dai due contatori all'uscita del cristallo. La relazione è nota come legge di Malus. In appendice c'è anche una breve introduzione ai vettori.
Ve ne eravate dimenticati? Sicuramente no... ma per un po' di tempo il perfido Dott. Nobody aveva lasciato in pace il nostro povero Pippo, come promessogli. Tuttavia, quando si è Nobody, ogni promessa NON viene mantenuta. Questa volta sembra che per Pippo la faccenda diventi molto difficile. Un problema che ci immerge (con tutte le cautele del caso) nell'ambiguità tra onda e particella. Insomma, un quiz, per così dire, quantistico.
Riprendo il discorso sulla disuguaglianza di Bell. In questo articolo iniziamo il percorso esaminando alcuni fatti riguardanti la polarizzazione dei fotoni. Questi fenomeni, noti fin da inizio 1800, hanno una interpretazione quantistica che ci permetterà di avvicinarci negli articoli successivi ad alcuni degli elementi che sono alla base della Interpretazione Standard. Inoltre alcune delle possibili disuguaglianze di Bell riguardano proprio un particolare fenomeno di polarizzazione di coppie di fotoni. È in base a queste disuguaglianze che sono stati condotti la maggior parte degli esperimenti, tra i quali quelli condotti da Alain Aspect, che hanno messo alla prova le interpretazioni locali della meccanica quantistica.
Parecchio tempo fa il nostro Fabrizio aveva esposto in modo molto sintetico e accattivante (più di 2000 lettori) la cosiddetta disuguaglianza di Bell, in grado di risolvere in modo giudicato empirico il celebre problema (o paradosso) sollevato da Einstein e colleghi (EPR), che sembrava distruggere la meccanica quantistica.
Il titolo è alquanto sibillino, ma vuol dire, in pratica, che se ci accorgiamo che la Natura rompe quella che noi consideravamo una perfetta simmetria, è molto facile che il modello da noi costruito sia sbagliato.
Riporto tre news in modo molto stringato, più che altro per dimostrare come spesso la prima soluzione non sia la migliore...
Tra le quattro interazioni (o forze) della Natura quella meno "visibile", ma forse più utile perché esista la materia, è quella nucleare forte. Una forza che si è dimostrata capace di adattarsi a condizioni critiche.