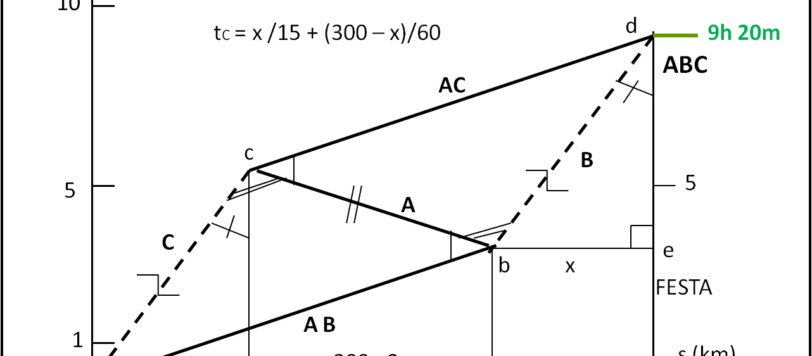
Quanta fatica, ma, alla fine, la montagna ha partorito il topolino (o viceversa). Ho voluto seguire una trattazione che è da un lato la più semplice e particolareggiata possibile, ma che da un altro sembrerebbe complicare le cose semplici. Sarete voi a dirmi se ho esagerato oppure no. Io penso che se tutti i grafici che vi sto per proporre saranno compresi completamente, le onde non porranno più problemi di sorta. Incrocio le dita...