Una ciliegina, ina... ina.... Però, chissà...


Divertiamoci ancora con il servizio nel gioco del tennis e sfruttiamo quanto già sappiamo sul moto di un proiettile: sport e cinematica si danno, ancora una volta, la mano.

Guardando una partita di tennis si può ragionare geometricamente, anche se in modo molto "rozzo".

Questo articolo è inserito in Dinamica e Meccanica ed è una delle tante "ciliegine" che potete gustare QUI Ammetto di aver forse dato, con una certa faciloneria semplificativa, una risposta non propriamente corretta a una domanda che mi è sicuramente stata fatta. Vorrei tentare di dare una risposta più vicina alla realtà dei fatti anche […]

Maurizio ha risposto correttamente. Ribadiamo la soluzione senza calcoli matematici e in modo qualitativo...

Questo articolo è già stato pubblicato e lo avevamo pensato come primo di una serie basata sulla libera traduzione di alcune delle celeberrime lezioni di fisica tenute da Richard Feynman alla Cornell University dal 1961 al 1964. Ma, nel momento in cui abbiamo provato a scrivere il seguito, ci siamo resi conto che il contributo originale alla comprensione della gravità si esaurisce in questa prima parte e andare avanti con una semplice opera di traduzione delle sue lezioni (peraltro già disponibile e facilmente acquistabile anche in rete), non ci sembra avere alcun valore aggiunto per i nostri lettori.
Riproponiamo, pertanto, questo articolo per riportarlo alla vostra attenzione e aggiungere una gocciolina all'oceano della divulgazione del Feynman-pensiero. Con l'occasione, lo inseriamo in quel vaso di Pandora che è l'archivio di questo Circolo-Blog, per la precisione nella sezione dedicata alla Dinamica e Meccanica in Fisica classica.

Vogliamo cercare di rendere più semplice possibile il tentativo di gettare un sasso in modo che riesca ad arrivare il più lontano possibile. Per riuscirci, utilizziamo un semplice metodo basato sulla geometria e su un pizzico di fisica classica.

Un premio Nobel più che giusto quello di Giorgio Parisi e fa un po' ridere che non molto tempo fa un virologo o immunologo o infettivologo, fate un po' voi, che è sempre presente in TV, lo abbia accusato, in modo più o meno trasparente, di non sapere leggere e interpretare i dati. Penso che oggi tale illustre personaggio televisivo avrebbe voluto mordersi la lingua, anche perché proprio i dati sono fondamentali per gli studi eseguiti da Parisi e che gli hanno valso il Nobel.

Spesso si parla di cattura di un oggetto che passi vicino a un pianeta. Sì, è possibile, ma solo se si intromette qualche altro oggetto o se si agisce su di lui.
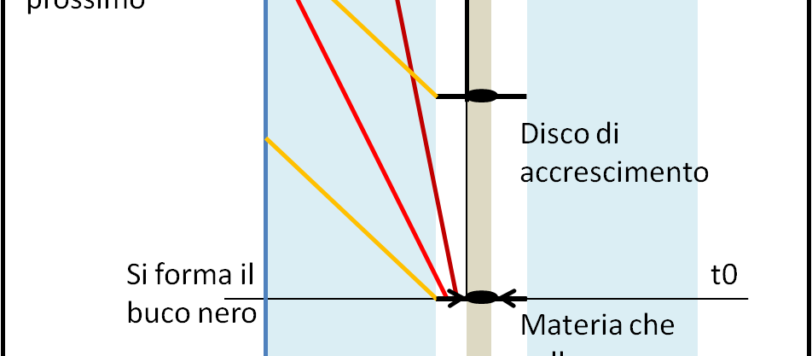
Torniamo ancora una volta allo spaziotempo vicino a un buco nero e azzardiamo una figura, con tutte le ovvie approssimazioni del caso...

Penso che qualcuno si ricorderà di un evento decisamente fantastico che avevamo riportato con il titolo di "accadde domani". In breve, si riportava un'osservazione, anzi più osservazioni, che avevano dell'incredibile: la stessa supernova si vedeva in tempi diversi e addirittura poteva (come si è riusciti a fare) essere prevista la sua esplosione in modo da assistere a tutto l'evento "in diretta".

Vorrei cercare di esprimere un concetto piuttosto sottile che mette in luce quanto la meccanica quantistica sia veramente necessaria per osservare l'Universo, ma anche quanto sia terribilmente "ambigua".

Sfatiamo, in qualche modo, una leggenda sui buchi bianchi che vengono, quasi sempre, identificati come buchi neri "al contrario", ossia come oggetti da cui esce di tutto e niente può entrarvi.
Ci poniamo una domanda: "E' veramente importante conoscere il centro di gravità di un insieme di oggetti celesti celeste formato da un numero molto alto di masse?". La risposta sembrerebbe essere: "SI". Accidenti, sappiamo benissimo che la legge di gravità impone una rivoluzione di ogni singolo oggetto attorno a un punto in cui può essere concentrata tutta la massa. E questo punto non può essere altro che il centro di gravità o baricentro dell'intero sistema. Teoricamente non fa una piega. Ma...