Facciamo girare le provette... un quiz -forse- leggermente più difficile, ma non è detto... basta riflettere.
La velocità più difficile da misurare? La velocità della luce. Lo sapeva anche Einstein e ha dovuto imporre una "convenzione" per sviluppare la sua teoria. E le cose non sono ancora cambiate...
Contrariamente a quello che può sembrare, lavorare nell'archivio più infinito del Cosmo, dispensando gradite sorprese, è tutt'altro che monotono.
E a volte capita che la gradita sorpresa sia talmente gradita da non poter non essere condivisa... ecco a voi, quindi, una presentazione pubblicata anni fa, alla quale non era ancora stato dato in archivio la visibilità che merita! Finalmente abbiamo rimediato.
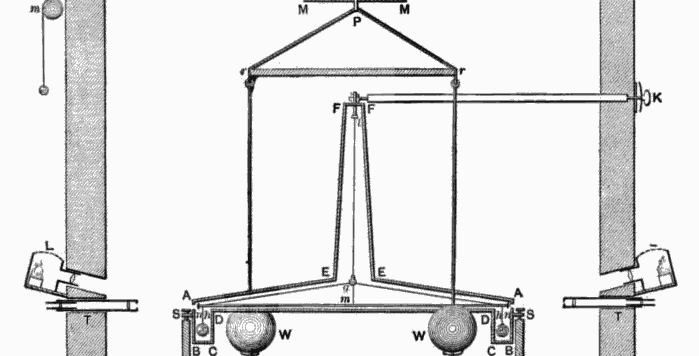
Newton scoprì una legge fondamentale e soprattutto universale per spiegare il moto dei pianeti e non solo, ma non riuscì mai a determinare il valore della sua costante G. Dovette quindi accontentarsi solo di rapporti di forze, in modo da eliminare quella scomoda costante, il cui valore fu ricavato solo un secolo e mezzo dopo grazie a sofisticatissimi strumenti di laboratorio e a piccole masse che, però, non servirono subito a determinare G, bensì la densità della Terra. Insomma, la storia di G è una lunga avventura nella quale il ruolo del protagonista è ricoperto dall'esperimento di Henry Cavendish del 1797-98 ed è questo che ci accingiamo a descrivere.
Per capire in modo molto rudimentale cosa siano effettivamente i tanto ricercati gravitoni (per adesso ancora soltanto ipotizzati) basta, in fondo, fare un paragone con i fotoni. Una piccola ciliegina estiva...
Questo quiz nasce per caso... stavo scrivendo un articolo dedicato al fantastico esperimento di Cavendish che ha permesso di calcolare la densità della Terra, quando mi sono accorto che per giungere alla descrizione completa era necessario risolvere un piccolo problema di ottica geometrica. Ho deciso perciò di non darlo come acquisito e nemmeno di dimostrarlo, ma di proporlo come quiz abbastanza rilassante durante questo periodo di ferie e di caldo. Chissà che qualcuno non abbia voglia di spendere un po' di tempo per risolverlo?
Inizia un progetto piuttosto ambizioso: la traduzione in modo molto libero -e ridotto- di alcune delle celeberrime lezioni sulla fisica base di Richard Feynman, tenute alla Cornell University dal 1961 al 1964. Un giusto ricordo di chi ha cercato, con tutto se stesso, di impartire interesse e capacità di ragionamento nei futuri uomini di pensiero. Tempo perso? Forse sì, ma mi basterebbe che anche un solo giovane trovasse spunto per cambiare la visione succube e passiva della propria esistenza.
Come tutte le grandi scoperte, spesso si esaspera la "prima volta" e poi si fa in fretta a dimenticare... Forse, qualcosa del genere sta succedendo anche per le onde gravitazionali.
Continuiamo nel racconto dell'avventura di Papallaccio e di come il suo gesto malvagio si ritorca contro di lui. Limitiamoci a una spiegazione estremamente qualitativa, dato che la faccenda è ben più complessa e ci farebbe entrare nelle manovre dinamiche che riguardano i satelliti artificiali.
Chi si offre volontario per verificare i calcoli del vulcanico (o vulcaniano?!?) Albertone?
La massa cresce andando sempre più veloci! Oh, mamma mia, come farò a volare tra le stelle e mantenere la linea?
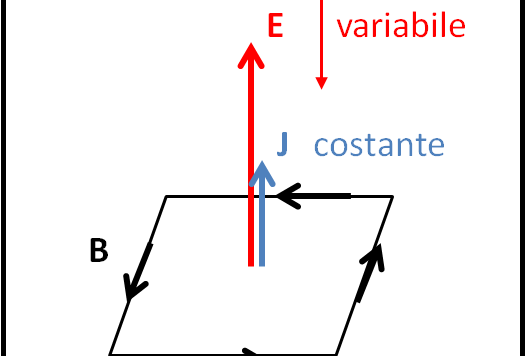
In questo articolo scriviamo le equazioni in versione differenziale, utilizzando i teoremi del rotore e della divergenza. Poi, tra un po', vedremo se risolvere le equazioni differenziali che portano alle onde elettromagnetiche...
una semplice, ma non banalissima, domanda di meccanica celeste o, meglio ancora, di astrodinamica. Non vi è bisogno di formule, ma solo di un po' di ragionamento..
Anche Albertino pensa di poter sbagliare... ma proprio quando cerca di correggersi commette il suo più grande errore. In ogni modo, è già nato chi sarà in grado di fare un passo successivo? Se speriamo solo nella materia ed energia oscura temo proprio di no.
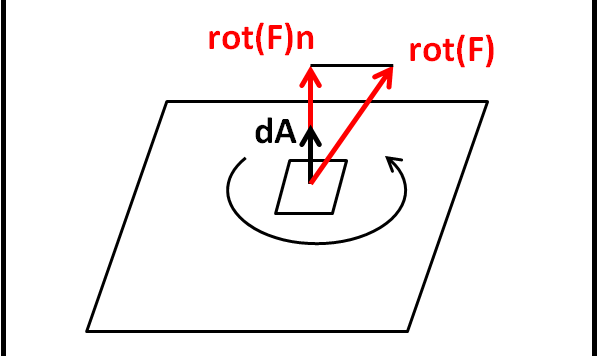
Descriviamo i due teoremi fondamentali (della divergenza e del rotore) che ci permetteranno di passare dalle equazioni di Maxwell in forma integrale a quelle in forma differenziale.
Se mando un segnale su Venere, posizionato dalla parte opposta del Sole rispetto alla Terra, e aspetto che torni indietro, mi accorgerò che il tempo impiegato è maggiore di quello calcolato teoricamente. Come mai? Basta tener presente che la luce è dovuta transitare due volte nei pressi del Sole... Ciò vuol forse dire che la velocità della luce è diminuita? Chiedetelo a Shapiro.