Concludiamo (per adesso, almeno) la nostra visita alle curve di Lissajous, analizzando in modo molto semplificato la loro applicazione naturale e artificiale, nel campo "terribile" della Meccanica Celeste.
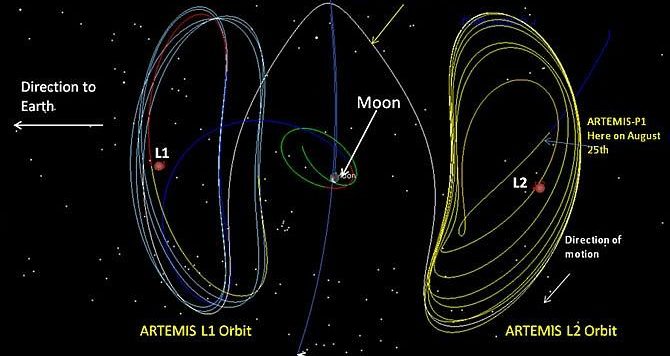

Concludiamo (per adesso, almeno) la nostra visita alle curve di Lissajous, analizzando in modo molto semplificato la loro applicazione naturale e artificiale, nel campo "terribile" della Meccanica Celeste.

Prendiamo in mano le nostre equazioni parametriche generali e cominciamo a vederne dei casi particolari. Ritroveremo quelle che già abbiamo trattato la volta scorsa, ma anche molte, molte altre... Potete costruirvele da soli o fare un programmino allo scopo.
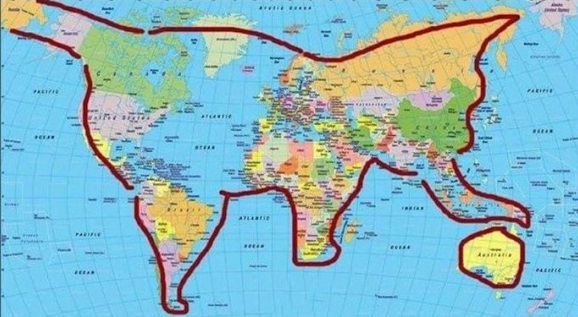
"La spiegazione del moto del gatto parmi assai semplice. Questo animale abbandonato a sé, descrive colla sua coda un cerchio nel piano perpendicolare all'asse del suo corpo. In conseguenza, pel principio delle aree, il resto del suo corpo deve rotare in senso opposto al moto della coda; e quando ha rotato della quantità voluta, egli ferma la sua coda e con ciò arresta contemporaneamente il moto suo rotatorio, salvando in tal guisa sé ed il principio delle aree" (Giuseppe Peano)

Prima di parlare di una ricerca che potrebbe essere fondamentale, voglio ricordare con grande affetto chi l'ha portata avanti: Mariateresa Crosta dell'Osservatorio di Torino. Ragazza estremamente capace, simpatica e intelligente, in cerca di un posto, ha lottato con la calma di chi è sicuro dei proprio mezzi e c'è riuscita. Oggi, inoltre, potrebbe avere smontato del tutto il comodo castello di carte su cui si basa la materia oscura. Un "brava!" a lei e un bravo anche a Mario, guida della missione Gaia.
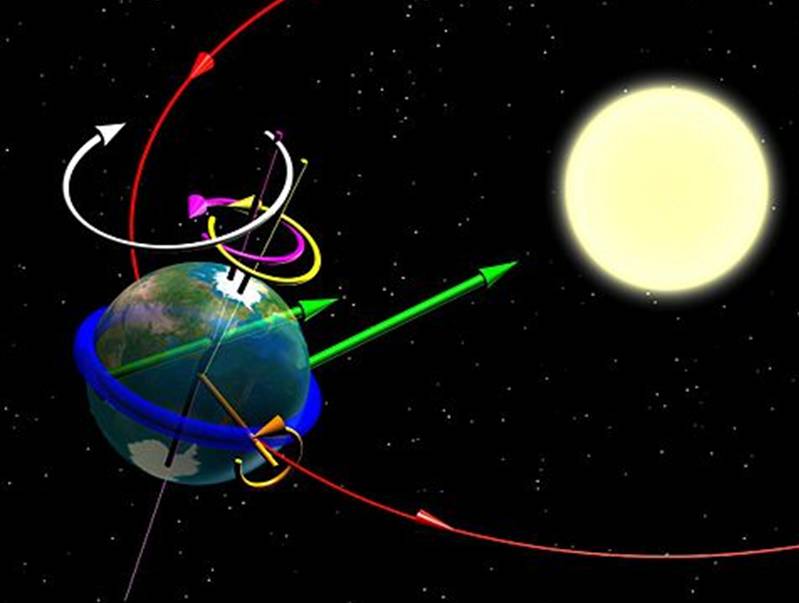
Tutti avranno sentito parlare di precessione almeno una volta. Essa viene citata sia quando di parla di spostamento della stella polare come indicatrice della direzione del polo nord sia quando si discute sul cambiamento delle costellazioni dello zodiaco sia, a volte, delle coordinate delle stelle. In qualche modo si parla di precessione solo per i suoi effetti, ma non riguardo alla sua vera ragione fisica. Eppure, la osserviamo sempre quando facciamo girare una trottola e i telescopi spaziali non potrebbero puntare esattamente gli oggetti celesti senza "trottole" molto speciali.

Se vogliamo dare rilevanza scientifica alla leggenda secondo la quale il gatto acquisì la capacità di cadere sempre in piedi grazie alla benedizione ricevuta da Maometto dopo avergli salvato la vita uccidendo il serpente che stava per morderlo, possiamo considerare il caso chiuso ed evitare di raccontare gli sforzi che, a partire dal '700, molti scienziati hanno profuso per comprendere le cause di questo apparente paradosso fisico. Ma, siccome siamo dei miscredenti e pure un pochino eretici, non ce ne voglia Maometto, ma li racconteremo!

Parliamoci chiaro, se Einstein avesse visto cadere un gatto invece che un imbianchino probabilmente la relatività generale non sarebbe mai nata... Le sue fondamentali deduzioni sulla caduta libera sarebbero andate a farsi benedire...

Sembra quasi la risposta all'articolo appena pubblicato. Quando c'è un unione di buchi neri molto lontani ci si può aspettare un segnale di onde gravitazionali, ma non un segnale elettromagnetico. Tutti d'accordo? Nemmeno per sogno ed ecco un caso che potrebbe rivoltare la situazione.

Nella soluzione che propongo a questo quiz ci si rifà pari pari alla formula trovata da Dirac, sia sostituendo pi greco al numero 2 sia scrivendo 2 in altro modo... Ringrazio ufficialmente Karl, Andy e Fabrizio per la volontà, l'interesse e le capacità dimostrate!

Potremmo dire che una ciambella cosmica ha mostrato -forse- di non avere il buco. Le onde gravitazionali hanno individuato un oggetto che non sarebbe né carne (buco nero) né pesce (stella di neutroni), secondo i dati osservativi precedenti all'evento.

Questa volta voglio accontentare i più bravi ed ecco un bel quiz matematico con quattro asterischi che possono anche diventare sei per i bravissimi (e molto fantasiosi).

Concludiamo l'avventura di Tarzan sia matematicamente che geometricamente, permettendo anche una costruzione meccanica (roba da ingegneri della giungla...)
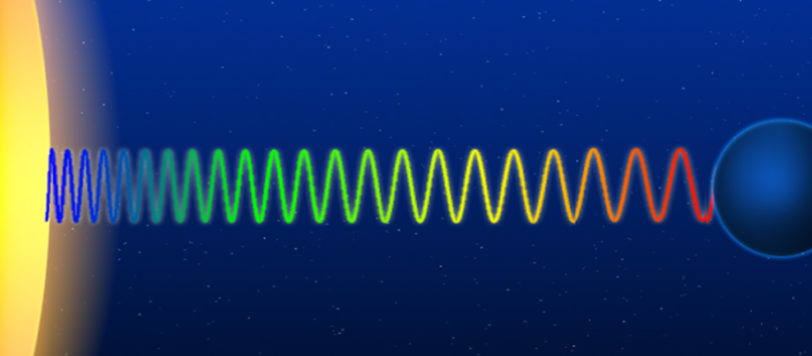
Una domanda che mi è stata fatta recentemente e che merita una risposta... Se ne potrebbero dare di diverso tipo, ma fatemi ragionare solo sfruttando la geometria dello spaziotempo.

Ebbene sì... proviamo finalmente a definire in modo molto semplificato (spero) il fantomatico "tensore" che tanta paura esercita in chi cerca di avvicinarlo. Lo facciamo in modo forse meno convenzionale, cercando di affrontarlo da un punto quasi puramente geometrico, sperando che i due asterischi diano la giusta quantificazione della sua effettiva difficoltà (ossia è articolo per TUTTI coloro che si sentano di dare del tu ai vettori). Pensiamo che sarà poi più semplice capirne le proprietà che lo rendono anche un "oggetto" di pura matematica. Inoltre, cerchiamo anche di approfittare di questa introduzione per capire ancora meglio sia l'importanza e la genialità concettuale della Relatività Generale, sia la difficoltà estrema che si cela dietro una formula finale dall'apparenza molto innocua.
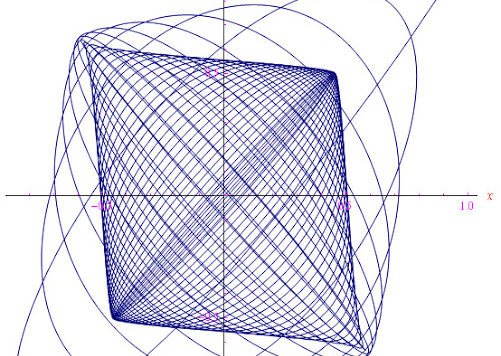
In questa prima parte torniamo un po' all'antica... ai bei tempi in cui cercavo di spiegare l'analisi matematica, con tanto di derivate e integrali, in modo comprensibile a tutti coloro dotati di voglia di imparare e di conoscere, per avendo basi di partenza molto basse (che male c'è?). Iniziamo perciò in modo veramente elementare e ci portiamo rapidamente e facilmente a maneggiare le celebri e bellissime figure di Lissajous. Per far contenti coloro che usano dire: "Sì, belle... ma a che servono?" toccheremo le applicazioni che le hanno portate ad essere fondamentali nel posizionare velivoli spaziali che necessitano di condizioni stabili e non vicinissime alla Terra. E se ce la sta facendo l'uomo, potete giurarci che non se l'è certo fatto scappare madre Natura!