Un problemino abbastanza facile che, però, può complicarsi un po' nello studio delle configurazioni possibili.
Facciamo chiarezza sul tempo del fotone...
Molto più strano (ma per fortuna sua e della Scienza anche molto più ricco) di Oliver Heaviside, ancor più timido di James Clerk Maxwell, perfino più schivo di Isaac Newton, con una voce sgradevolmente stridula almeno quanto quella di Alan Turing, HENRY CAVENDISH nacque nel 1731 e, nell’arco della sua lunga vita (morì nel 1810) pesò, numerò e misurò tutto ciò che fu per lui possibile pesare, numerare e misurare!
La Lagrangiana sta diventando sempre più necessaria in tutti i problemi di fisica. In fondo, basta compiere la minima... azione!
Il numero di persone che "sanno" cos'è il problema dei tre corpi sta aumentando a dismisura. Un nuovo interesse per la fisica? Purtroppo no... la colpa (o il merito) è di un romanzo di fantascienza (e della relativa serie TV). Parliamone...
Cosa succede all'interno di un buco nero? Einstein non può dircelo, ma la meccanica quantistica può anche immaginarlo... Forse, forse, i buchi neri non rubano le informazioni!
L'agente 007, alias James Bond, sta andando a salvare il mondo... Per far ciò deve ricevere un documento importantissimo. Ce la farà?
Teoria dei campi quantici? un argomento estremamente complesso e ben poco intuitivo. Particelle virtuali? Idem come sopra. Beh, questo articolo vuole cercare di semplificare (forse troppo) i concetti di base. Consideriamolo una semplice ciliegina subatomica.
La soluzione poteva essere quasi immediata anche per via analitica. Basta pensare a una .piuma ...
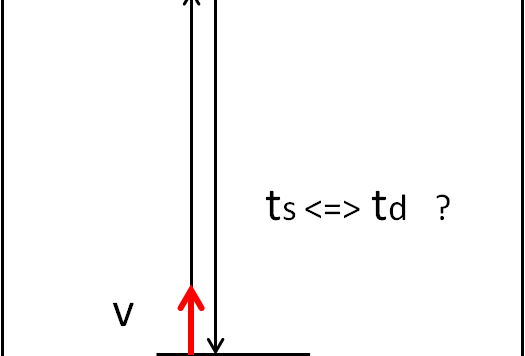
Feynman proponeva spesso esercizi di fisica all'apparenza banali. Eccone uno decisamente semplice, ma...
Un semplice problema di cinematica che ci permette di colpire il nemico mentre sale su una collina.
E se le ruote fossero rimaste quadrate? Poco male... bastava modificare le strade.
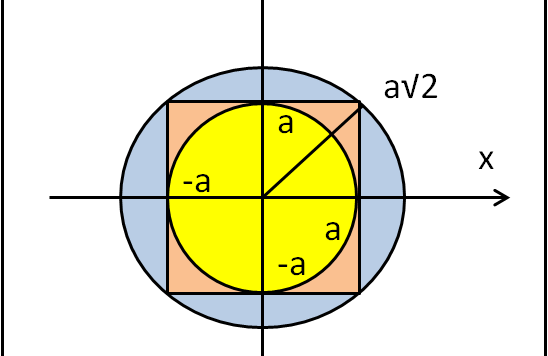
A Gauss piacevano gli integrali doppi e attraverso di essi ha risolto un integrale "semplice" che sembrava impossibile. Un integrale fondamentale nel calcolo statistico dato che si riferisce proprio alla gaussiana, ossia alla distribuzione delle probabilità dei valori che una variabile può assumere. Ad esempio: misurando l'altezza delle persone ci regala l'altezza media e lo scarto relativo a tale valore. In altre parole, non vi è campo della Scienza che non abbia bisogno della distribuzione gaussiana, detta anche "normale".
Una corda sospesa... vi ricorda qualcosa?
Scivolando verso la vittoria Una delle azioni più spettacolari nel gioco del baseball è la conquista di una base in “scivolata”, una prodezza che richiede un certo talento, ed ha lo scopo di eludere la minaccia del difensore della base, scomparendo letteralmente dal suo orizzonte. Il giocatore in difesa, a cui i compagni […]
Un esercizio molto utile per comprendere al meglio i momenti d'inerzia e quelli angolari.