Le onde gravitazionali fanno sempre meno notizia. Un bene perché significa che le scoperte crescono e un male perché forse fa perdere di vista l'eccezionalità della loro rilevazione.
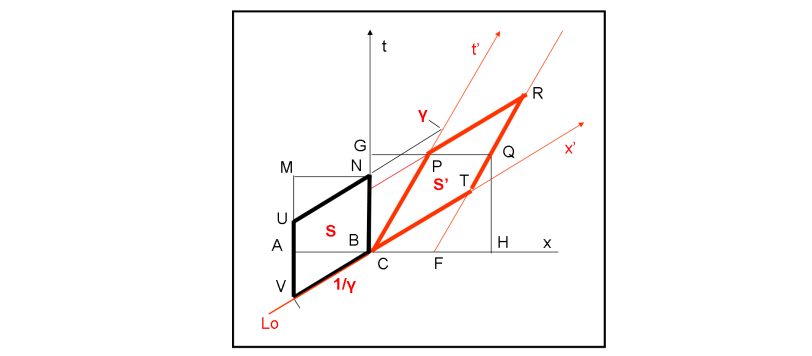
Per questo breve articolo ringrazio il caro lettore Giovanni che, giustamente, in un commento ha evidenziato quanto sia, generalmente, poco citata l'invarianza delle aree nello spaziotempo di Minkowski. Una lacuna che ci conduce a un semplice gioco essenzialmente geometrico.
Siamo nel 2570 d.C. e un gruppo di turisti si è recato sul pianeta “Paradise” per ammirare la fantastica flora e fauna di quel mondo alieno. L’astronave che li ha portati tornerà a riprenderli molti mesi dopo e si trova a distanza enorme da loro. Ma ecco un fenomeno imprevisto e non certo piacevole per chi sta sul pianeta... non c'è tempo da perdere!
Un altro semplice esercizio di relatività speciale. Qualche piccolo calcolo e via!
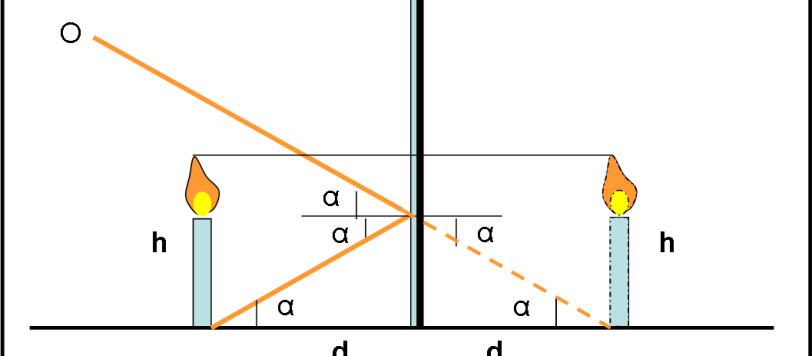
Fa sempre bene richiamare un po’ di ottica geometrica e questo non-quiz serve solo come piccolo ripasso.
Non voglio sicuramente ricominciare a trattare la relatività ristretta che trova ampio spazio nell'archivio. Tuttavia, avendo visto che lo spaziotempo di Minkowski è l'articolo più letto del nostro Circolo, mi è sembrato giusto tastare un po' il polso dei lettori che l'hanno affrontato. Per far ciò, vorrei presentare qualche esercizio di grande semplicità, ma sufficiente a mettere alla prova le conoscenze raggiunte, soprattutto nelle questioni fondamentali: chiamerò questa serie "Minkowski per tutti". Conoscendo la reticenza dei più nell'uscire allo scoperto, non mi aspetto molte risposte "pubbliche", ma sono sicuro che privatamente molti cercheranno di risolverli. Le risposte si possono ottenere schiacciando su "mostra risposta", ma... chi è relativamente speciale non lo farà di certo!
Grande rivoluzione nel mondo delle unità di misura. Dal 20 maggio 2019 avremo ufficialmente sette unità fondamentali, tutte immutabili perché legate a valori di costanti fisiche universali. Potremo dialogare di fisica con gli alieni senza farci ridere dietro, dicendo che per noi il chilo è il peso di quel cilindro di metallo che teniamo sotto doppia campana di vetro a Parigi.
Un quiz non quiz che riguarda un dramma spaziale. Proprio per la sua semplicità e per il valore didattico aspetteremo un paio di giorni prima di inserire la risposta. Provate a risolverlo, così valuterete la vostra comprensione dei principi base della relatività speciale e farete contento il Dott. Einstein… In seguito, passeremo al diagramma di Minkowski e spero che tutti i nostri lettori gli daranno del tu come a un vecchio amico.
Un piccolo esercizio di meccanica classica per i nostri amici astronauti sempre in giro per conoscere le meraviglie dell'Universo. Un problema, tuttavia, che viene normalmente affrontato anche nella realtà.
Per stabilire chi è il vincitore tra Achille e la Tartaruga bisogna normalmente passare ai limite oppure farli andare sui campi da sci. Molto più semplice è invece stabilire il vincitore tra una Tartaruga-muone (ad esempio) e un Achille-fotone. E tutto avviene in silenzio senza dover aspettare che venga frantumato il solito muro del suono.
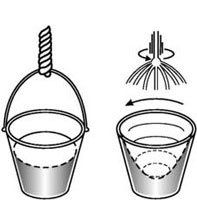
A volte, in fisica, vi sono fenomeni che possono sembrare, a prima vista, contro intuitivi. Ne presentiamo uno che è una specie di classico in tal senso...
In un racconto di Vin-Census avevamo visto trasformare la Terra, suo malgrado, in un deposito di spazzatura spaziale. Una fantascienza che potrebbe anche diventare realtà in un futuro molto lontano. Tuttavia, già adesso, sembra che la faccenda possa prendere una piega interessante e/o spaventosa (a seconda dei punti di vista).
Sembra quasi che la prestigiosa rivista inglese MNRAS abbia risposto alla mia teoria basata su Maga Magò... Non tutti si affidano alle costruzioni fittizie, usandole poi come metro di conferma. C'è ancora chi si affida ai dati, alle teorie ben confermate e ad analisi attente e prolungate nel tempo...
Chi l'avrebbe mai detto? Il tarassaco o dente di leone che spesso invade interi prati con i suoi fiori gialli potrebbe diventare uno dei pionieri di un nuovo tipo di volo... Forza botanici e ingegneri, dateci dentro! Le applicazioni pratiche non sono poi così lontane. In fondo lo scopo è sempre quello: volare nel vento e cercare tante risposte ...
Uno dei tipi di telescopio più famosi porta il nome di uno scienziato altrettanto famoso. La sua caratteristica principale è l’obiettivo formato da uno specchio che ha una particolare forma, capace di eliminare un certo tipo di difetto che limita le prestazioni del suo compagno “sferico”. Teoricamente (ma anche praticamente), chiunque può costruire “in casa” questo tipo di obiettivo (il metodo è stato utilizzato professionalmente).
La riflessione di un "qualcosa" sulla superficie di un lago o di un mare, porta a qualche semplice, ma istruttiva riflessione sulla riflessione luminosa. Parliamone allegramente...