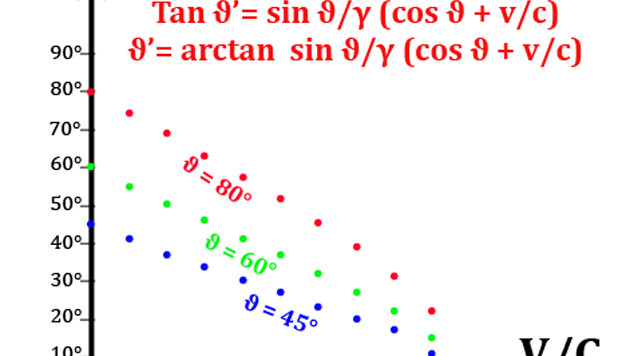
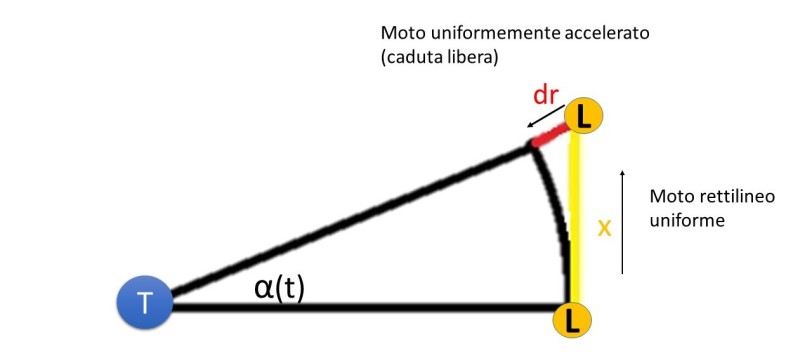
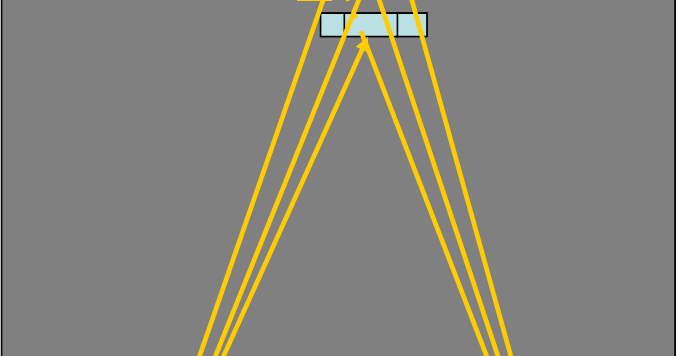
Fabricius usa la pietra Lagrangiana per risolvere i problemi. Con la parola magica KappaU li chiude nella pietra che colpita dalla luce Eulgrange emette la soluzione. Noi ci dobbiamo accontentare del metodo di Lagrange che attraverso l'energia cinetica (K) e l'energia potenziale (U) ci fa costruire la lagrangiana. La lagrangiana elaborata con l'equazione di Eulero-Lagrange ci fornisce la soluzione.
Nelle puntate precedenti abbiamo costruito alcuni esempi di lagrangiane di corpi liberi e vincolati ed abbiamo preso confidenza con le derivate che sono utilizzate nella equazione di Eulero-Lagrange.
In questa quinta parte dell'articolo finalmente arriviamo alla equazione di Eulero-Lagrange.