Pensavo fosse più semplice di quanto dimostratosi. I miei ringraziamenti, comunque, vanno a Michele e Mau per averci provato! Il quiz diventa un utile ripasso del piano inclinato...
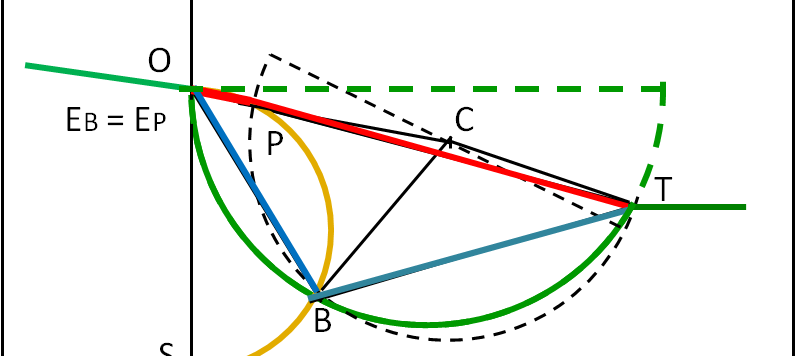

Pensavo fosse più semplice di quanto dimostratosi. I miei ringraziamenti, comunque, vanno a Michele e Mau per averci provato! Il quiz diventa un utile ripasso del piano inclinato...
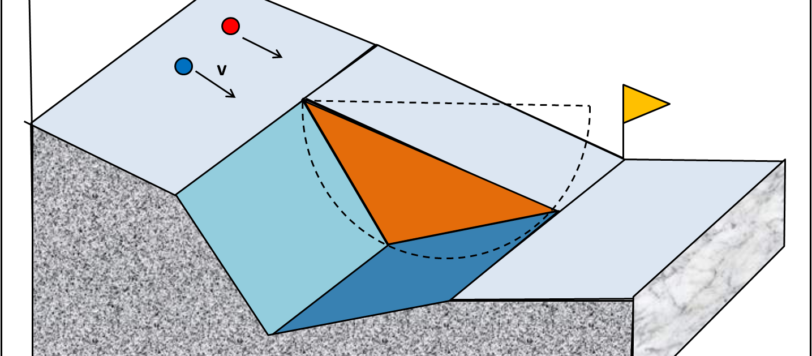
Dopo aver svolto insieme un certo numero di esercizi, è ora di mettervi alla prova sulla cinematica. Un'occasione per conoscere i due personaggi che hanno dato luogo al mio libro divulgativo di meccanica.
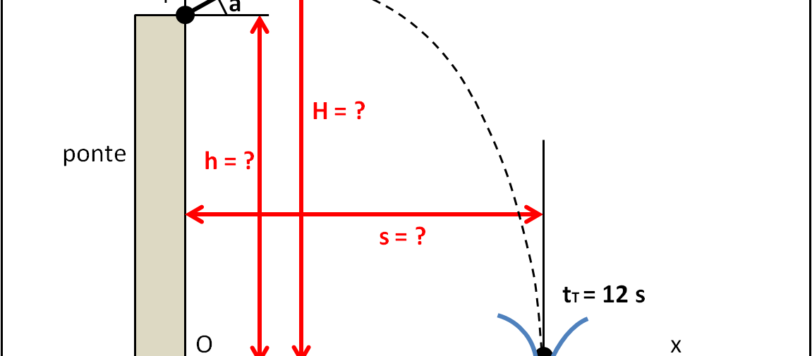
Ancora un paio di esercizi svolti assieme sulla cinematica bidimensionale e poi passeremo a un paio di quiz per mettere alla prova i meno esperti. Fatto questo ci occuperemo del moto circolare uniforme.
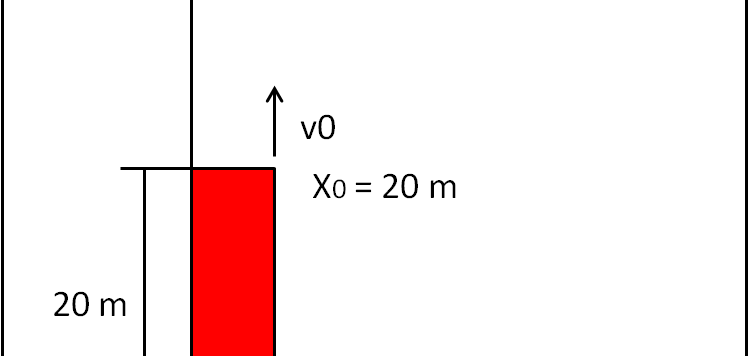
Un paio di esercizi di moto uniformemente accelerato, con l'applicazione della formula di Torricelli.
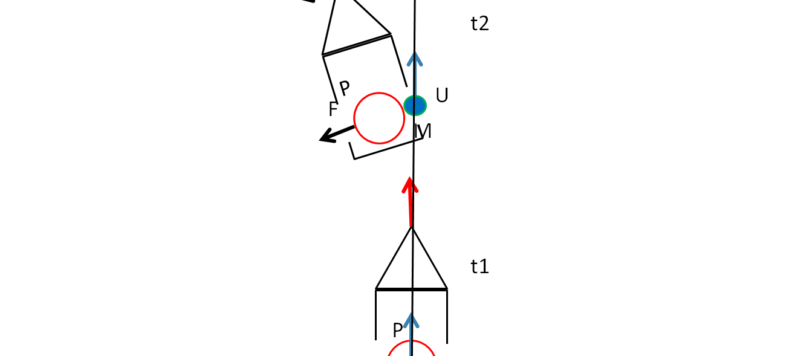
Il nostro amico Michele mi ha da poco chiesto di spiegare nel modo più semplice possibile la differenza tra forza centrifuga e centripeta, gioia e dolore di molti. Ho deciso di accontentarlo utilizzando solo la cinematica, in modo un po' empirico, senza formule, ma solo con il ragionamento e qualche figura. Spero di aver accontentato lui e -magari- qualche altro lettore.
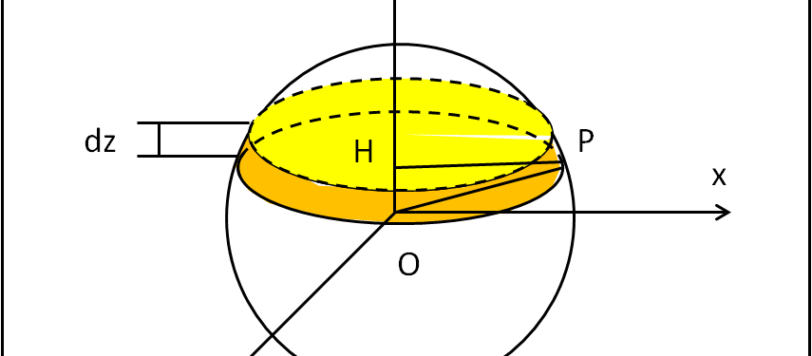
Proseguiamo il calcolo dei momenti d'inerzia passando alla sfera piena e al guscio sferico sottile.
Un eccezionale esperimento, svoltosi al CERN, ha mostrato che l'antimateria subisce la gravità come la materia.
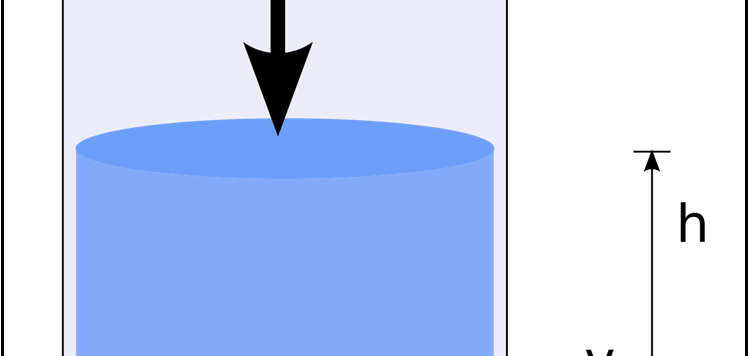
Continuiamo con la cinematica, aggiungendo una formula particolarmente utile per risolvere problemi con moto uniformemente accelerato. Non stupisca se c'è di mezzo Torricelli.
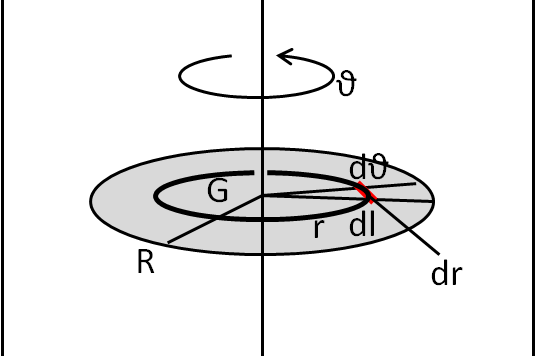
Continuiamo con i nostri momenti d'inerzia. Questa volta tocca all'anello sottile e al disco sottile.
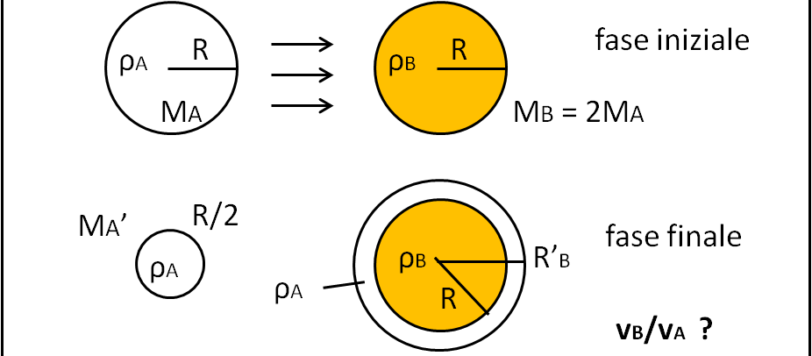
Un problema estratto da uno dei test di ammissione più difficili al mondo. Risolviamolo assieme...

Fabrizio ha centrato il bersaglio al primo colpo. Durante la prossima nevicata chiederemo consiglio a lui per organizzare la pulizia delle strade!
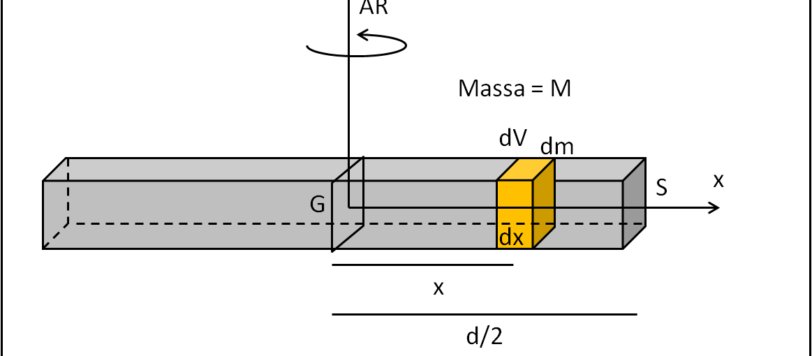
Negli svariati articoli di fisica classica, abbiamo sempre trascurato un po' il momento d'inerzia, ossia la "reazione" di un corpo a qualcosa che vuole farlo ruotare. Qualcosa, perciò, che è l'equivalente della massa in un moto traslatorio. Analizziamo da vicino e vediamo di calcolare i momenti d'inerzia di alcuni corpi rigidi con forme differenti. Iniziamo con una barretta di ferro...
Proseguendo nell'esecuzione di semplici esercizi di cinematica è meglio tener conto di possibili errori nell'applicazione delle formule fondamentali della cinematica.

Anche se intento a preparare semplici esercizi di cinematica e , in generale, di fisica classica, non potevo lasciare inoperosi i più esperti siano essi silenziosi oppure no. Chiamiamolo pure ... un anticipo di inverno!