La soluzione della seconda parte del quiz potrebbe essere data velocemente, ricordando alcune formule fondamentali della caduta di un corpo per effetto della gravità. Tuttavia, ho cercato di richiamare questo moto così importante, partendo praticamente da zero e mostrando come la sola caduta possa farci capire che l’intero esercizio può essere risolto sfruttando quasi solamente il puro ragionamento, utilizzando poche formule in modo ripetitivo. La trattazione potrebbe sembrare lunga e strabordante, ma leggendola attentamente ci si accorge di essere in grado, alla fine, di estendere i risultati a molti casi particolari. Una soluzione, perciò, costruita soprattutto per i meno preparati che abbiano voglia di ragionare…
Abbiamo parlato spesso di urti completamente elastici e anche un po’ di quelli completamente anelastici (nella dinamica relativistica). Vale la pena, però, descrivere gli urti in modo più generale, partendo dagli urti anelastici, proprio il caso che ci serve per il quiz sul papallo-canguro.
Dopo tanta relatività, torniamo un po’ alla fisica classica con un quiz tipicamente papalliano. Si chiedono varie risposte, che necessitano di un minimo di dinamica (classica) e qualcosa di matematica (un bel ripassino). I più bravi… aspettino qualche giorno.
Permettiamoci ancora un piccolo “scherzo”, richiamando la particella più strana e più simpatica dell’Universo: il fotone. Questo articolo conclude la dinamica relativistica, che, al più presto, metteremo tutta assieme negli approfondimenti.

Questo celebre discorso è già stato proposto nel Circolo in versione integrale e in lingua originale. Data la sua importanza e visto che in rete non se ne trova una versione in italiano, per far sì che ogni lettore abbia la possibilità di apprezzarlo, ci siamo rimboccati le maniche e, con grande piacere, lo abbiamo tradotto noi. Buona lettura!
Risolviamo il problema delle trasformazioni e ci accorgiamo che le formule sono esattamente le stesse che avevamo ottenuto trasformando t in t’ e x in x’.
La fantascientifica idea (ma non poi tanto) che vede in qualche modo coinvolto Hawking (soprattutto per rendere l’operazione fortemente mediatica) ci potrà permettere di mandare moltissime sonde su Alpha Centauri in un tempo non superiore a circa 20 anni. E magari, anche meno… La missione sfrutta un’amica di cui abbiamo parlato spesso ultimamente: la quantità di moto (e la sua conservazione).
Potevamo fermarci con l’articolo precedente. Tuttavia, non è male introdurre un QUIZ molto istruttivo. Anche senza tentare di risolverlo, è utilissimo seguirlo passo dopo passo. La soluzione alla prossima puntata.
Ancora una volta non ci sarebbe bisogno di dare la soluzione, tanto sono stati bravi i nostri esperti relativistici. Ne approfitto, perciò, per riproporre un’avventura spaziale che presenta l’orologio a luce e lo offre in un piatto d’argento per la soluzione geometrica finale.
Avete notato cosa succede quando un cane morde una persona? Diventa subito notizia da prima pagina e, improvvisamente, tutti i cani cominciano a mordere a destra e a sinistra. I media hanno attirato l’attenzione e allora tutti a cercare di mantenere calda la smania di un nuovo morso, anche se -magari- i vari eventi sono accaduti in tempi precedenti o addirittura sono stati inventati o ingigantiti. Purtroppo, anche nella scienza, quando si scopre qualcosa di nuovo, e che può attirare fondi e visibilità, vi è un assalto alla diligenza e tutti cercano di essere in prima fila, anche a costo di riproporre come novità progetti già datati. Poi c’è sempre chi si confonde, ma nessuno lo aiuta a chiarirsi le idee.
Iniziamo, ponendo il quiz senza dare nessuno aiuto, tranne il dire che è necessario ricordarsi molto bene l’orologio a luce. Poi, tutto si risolve con un triangolo rettangolo a cui si applica il teorema di Pitagora. Non c’è bisogno di nessuna formula, ma solo di un po’ di geometria. Un bell’esercizio per capire bene il legame tra orologio a luce, il fattore gamma e la sua applicazione al diagramma di Minkowski. Poi, giuro, che vi lascio in pace (per un po’ almeno…). In caso di particolare difficoltà, inseriremo una parte capace di semplificare il problema...
Non ce ne sarebbe nemmeno bisogno, dato che la soluzione è stata “azzeccata” praticamente da tutti quelli che hanno risposto (chi subito, chi con un paio di passaggi). Tuttavia, la ripropongo velocemente.
Questo articolo vuole solo essere un piccolo assaggio di quello che un giorno vorrei descrivere con molta calma e attenzione. Un legame strettissimo tra relatività ristretta e meccanica quantistica che ha portato a conseguenze quasi impensabili. Così, un piccolo stuzzichino, tanto per gradire...
Cosa c’è di meglio di un bel paradosso per fare un po’ di ripasso della relatività ristretta? Ne presento uno che è alla base di tutta la rappresentazione grafica di Minkowski. Forse è stato proprio lui a dare il via al celebre diagramma.
Fatemi arrivare al dunque in modo molto personale e “quasi” allegro e spontaneo. Abbiamo incontrato lungo il percorso nuove grandezze che dipendono dalla velocità. Grandezze che cambiano, cambiando sistema di riferimento. Ciò che viene conservato sono le loro leggi di … conservazione. D’altra parte siamo o non siamo nella relatività ristretta? Tuttavia, pensandoci bene, qualcosa che non cambia c’è e questo fatto implica un nuovo invariante che lega l’energia con la mia grandezza preferita.
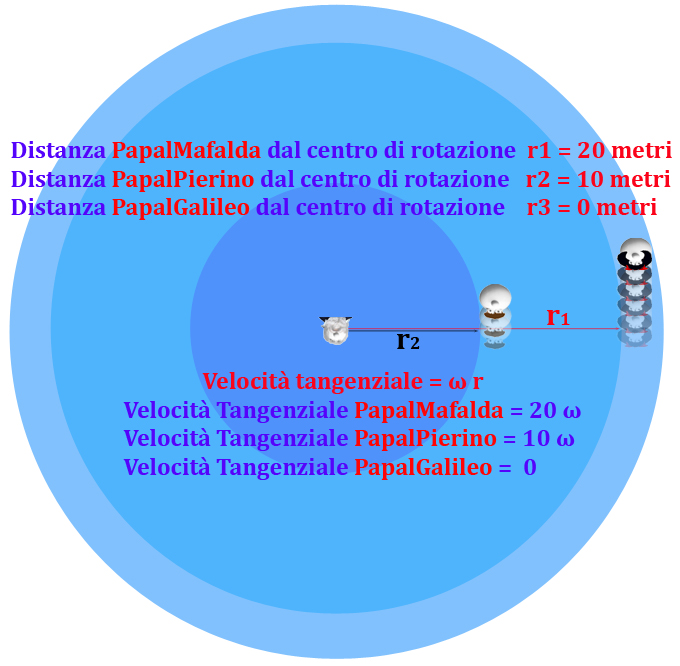
Considerato che in molti commenti al quiz è stata proposta una soluzione basata sulla forza centrifuga, ai papalli sembra giusto consentire a tutti di capire almeno di cosa si tratta. Chi si avvicina al mondo di Papalla rischia di perdersi quando le cose si complicano, meglio fare un passettino per volta … poi gioco dopo […]

