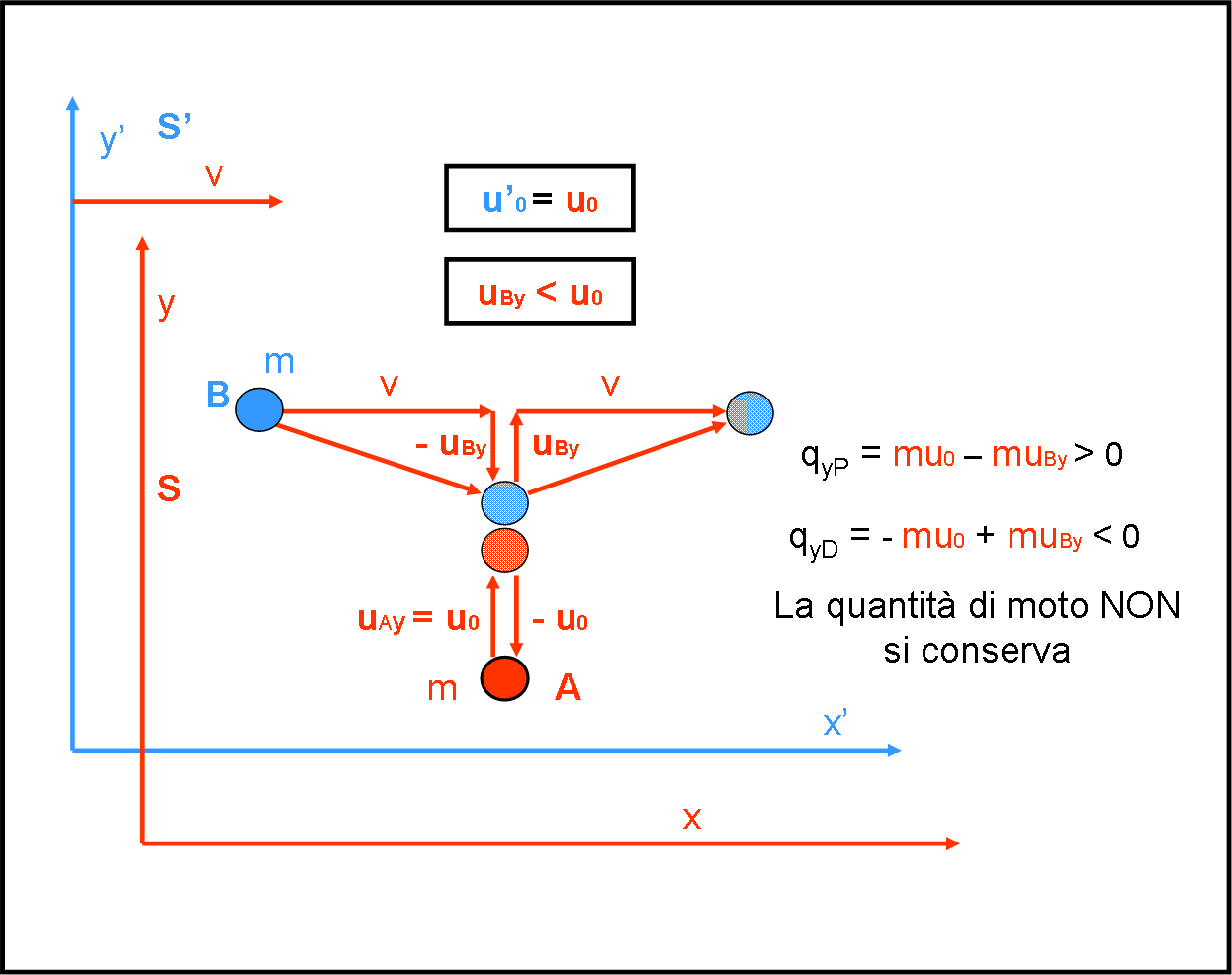
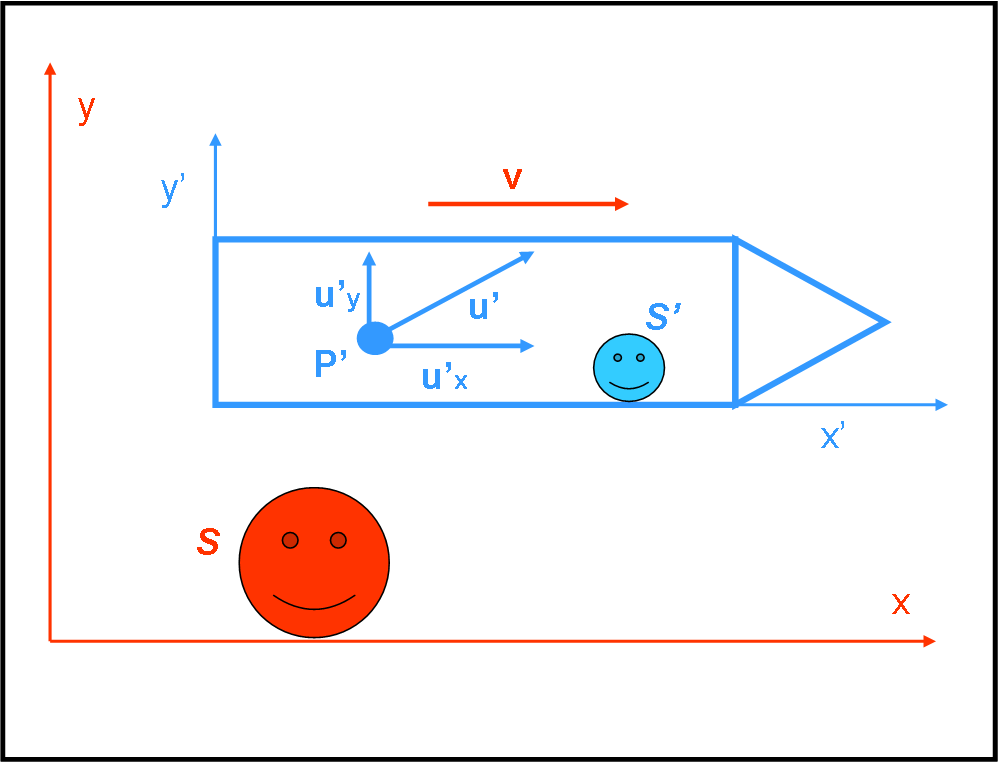
Questo articolo è molto corto. Preferiamo mangiare la “torta” a piccoli tranci per permetterci di gustarla fino in fondo. Dimostrare che la quantità di moto “classica” non si conserva nella Relatività Ristretta è un punto di arrivo fondamentale e va compreso perfettamente bene. Una conclusione, in realtà, banale, ma che ci obbliga a modificare tutta la dinamica conosciuta fino ad allora. Ricordiamo, comunque, che stiamo parlando di velocità comparabili a quella della luce. Se giocassimo a palline con un nostro amico che va in bicicletta niente cambierebbe rispetto alle descrizioni di Galileo.