Per parlare di onde gravitazionali bisognerebbe avere ben chiara la Relatività Generale e tutte le sue formule. Tuttavia, per gli scopi attuali di questo circolo possiamo usare delle spiegazioni semplificate (ci sarà tempo per renderle sempre più tecniche). Ho notato un po’ di confusione e, allora, cerco di eliminare i dubbi principali. Non prendete la trattazione, però, come qualcos di veramente “professionale”…
Tempo fa avevamo parlato di esperimenti eseguiti da studenti attraverso palloni aerostatici per lo studio della sopravvivenza di batteri terrestri in condizioni simili allo spazio interplanetario. Siamo ancora in attesa delle risposte definitive, ma il lavoro del gruppo estremamente attivo continua a bordo degli aerei di linea. Siamo in tempo di ferie e una fiala piena di bollicine dovrebbe farci riflettere un poco…
Pescare le onde gravitazionali è come pescare un grosso e furbissimo pesce. Ci vuole molta sensibilità e il luogo adatto. Il nuovo LIGO forse ci riuscirà a fine anno, pescando negli ammassi globulari.
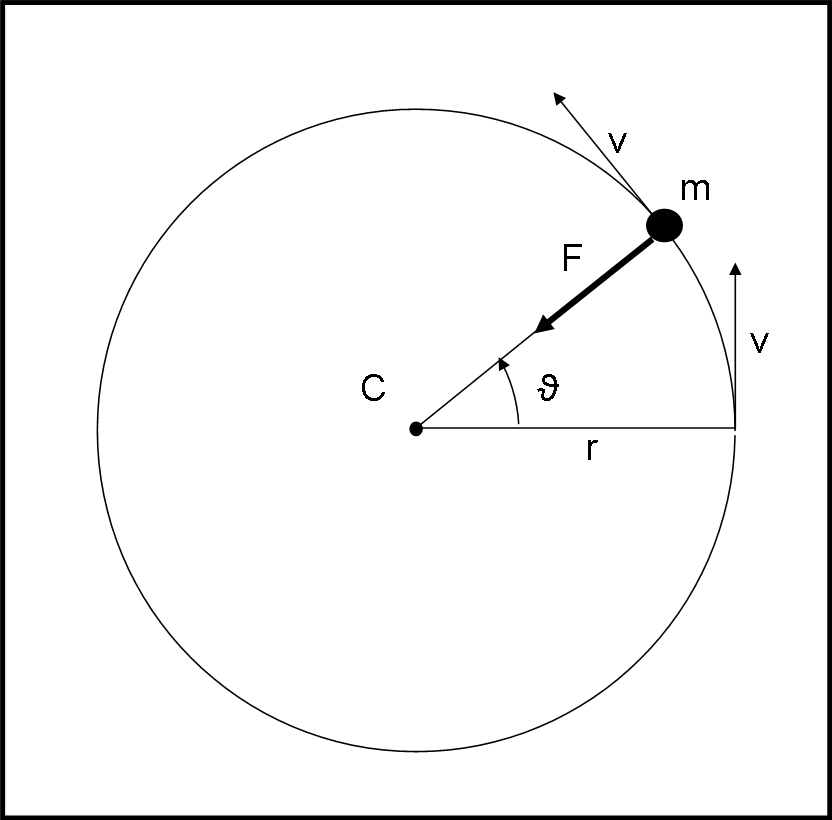
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.
Scrivo questo articoletto veramente elementare per farmi perdonare la dimenticanza di un dato fondamentale nel quiz sulla Terra “strana”. Farà ridere la maggior parte di voi, ma potrebbe anche servire a chi è proprio alle prime armi (o magari per raccontare la storia ai bambini). E’ in pratica la soluzione del quiz (impostato correttamente) riportata sotto forma di racconto e ambientato sulla nostra solita Papalla, pianeta del tutto simile alla Terra tranne che per un qualcosa … che facciamo cambiare di volta in volta.
Ho fatto un terribile pasticcio e ho reso difficile una risposta che tutti sapevate sicuramente dare. Chiedo umilmente scusa...
Finora si è sempre pensato che il fenomeno dell’entanglement, che tanto ha fatto arrabbiare Einstein, fosse strettamente legato alle particelle che vivono nel regime della meccanica quantistica. Il gatto di Schoedinger forniva un ottimo esempio per la creazione di un certo limite tra il mondo classico e quello quantico. Tuttavia, sembra che la faccenda sia molto più complicata (o forse molto più semplice). L’entanglement sembra essere una caratteristica che invade tranquillamente il mondo classico.
Staccati finalmente da cordoni ombelicali di dubbia utilità, mi permetto di fare un ulteriore esempio di inutili discussioni, dovute alla assoluta mancanza di basi di partenza. Cari ragazzi, per capire le meraviglie del cosmo e della mente umana (quando vuole lavorare veramente) ci vuole molta pazienza, logica e umiltà! E' necessario capire prima di esprimersi a casaccio o quasi... Io cerco solo, in tutta umiltà, di darvi i mezzi per farlo.
Concludiamo la parte dedicata alla descrizione geometrica della Relatività Ristretta attraverso il diagramma di Minkowski, introducendo un concetto di portata ben più generale, quello di Universo degli Eventi. Inoltre ci divertiamo un poco con l’invariante spaziotemporale, risolvendo, tra l’altro, il quiz sulla distanza spaziotemporale AB. Un articolo abbastanza fondamentale (riguardo al significato più profondo del diagramma) che ci porta al cono di luce e alla rappresentazione globale di tutto l'Universo. E' anche piuttosto lungo, anche se non difficile: digeritelo bene, mi raccomando...
Un quiz, dall’apparenza complicata, che diventa banale ragionando logicamente sull’invariante relativistico. Avete una settimana di tempo per rispondere. Chi lo farà può dire di aver compreso appieno il diagramma di Minkowski.
Avrei voluto aspettare un po’ a dare la soluzione grafica di questo quiz dal titolo molto sconvolgente. Abbiamo descritto la RR partendo dall’ipotesi che la velocità della luce sia costante in tutti i sistemi di riferimento e ora sembra che si sia trovato che non è affatto vero. Per non rischiare di creare uno stato confusionario, mi sento obbligato a dimostrare subito che la relatività della velocità della luce è solo un’apparenza dovuta al fatto che se cambia il tempo bisogna anche tener conto che cambia lo spazio…Ovviamente, chi vuole continuare a provare da solo (e lo spero veramente) non legga ancora questo articolo.
La velocità della luce deve essere la stessa in qualsiasi sistema di riferimento. Se non fosse così, dovremmo “bocciare” la relatività speciale… E, invece, i soliti problemi di simultaneità sembrano portare a un risultato sconvolgente. Quello che vi propongo è un piccolo esercizio di ripasso sull’utilizzo del diagramma di Minkowski. Sono cose che abbiamo già disegnato e discusso, ma è un buon “test” di prova.
Piccoli accenni e tentativi di stimolare, purtroppo, non servono a molto. Valgono molto più l’orgoglio e un po’ di menefreghismo. E allora, seguendo le giuste regole del buon divulgatore (a cui spero sempre più di avvicinarmi) ho scelto la strada più scientifica e produttiva: quella della spiegazione di un concetto che sta facendo cadere sempre più nella confusione e nella paura di azzardare critiche aperte e costruttive. Non mi interessa chi e come ha fatto sorgere la confusione. Il mio compito donchisciottesco è quello ci cercare di proporre una spiegazione più chiara e comprensibile possibile. Niente di più (chissà quando sarò compreso?) e niente di paranoico. Chi ha dubbi li esponga chiaramente. Nel caso potrei anche dire di avere sbagliato tutto. Non sono mai stato e mai sarò un genio come Leonardo o Feynman… Di fronte alla fisica e all’astrofisica sono un semplice studente delle scuole inferiori e devo ancora studiare tanto… Se sbaglio, vi prego, correggetemi!
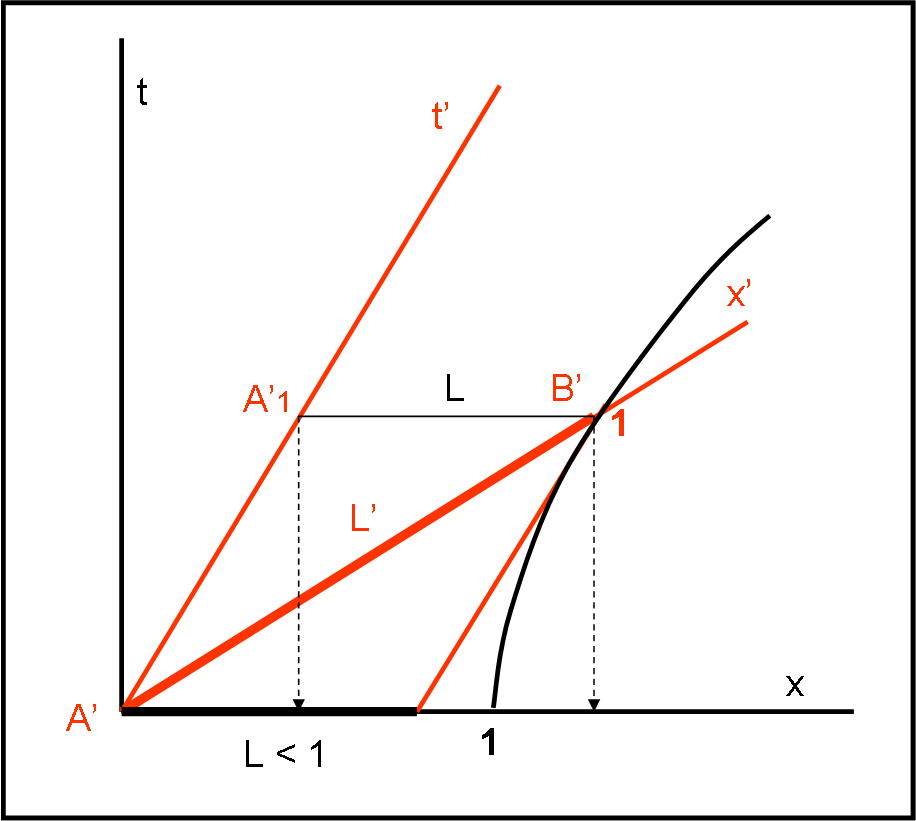
Dopo aver dilatato i tempi, divertiamoci, adesso, a contrarre le lunghezze, sempre per via puramente grafica. La dimostrazione è leggermente più complicata di quella precedente (ma tutto si basa sempre sulla necessità di usare più orologi). Come vedremo bisogna passare, prima, attraverso il tempo per arrivare, infine, alle lunghezze. Inoltre, solo la curva di calibrazione ci permetterà di capire che il nostro occhio, abituato alla geometria euclidea, può facilmente sbagliare…
Dopo aver divagato un poco con il paradosso dei gemelli, torniamo al nostro diagramma di Minkowski e iniziamo a vedere come sia facile ottenere graficamente la dilatazione dei tempi e la contrazione delle lunghezze. Ricordate che è fondamentale aver compreso bene il concetto di relatività della simultaneità e poco altro. Iniziamo con la parte più semplice, quella che riguarda la dilatazione dei tempi.
Ormai lo conosciamo bene… Il nostro Alvy non si accontenta mai delle cose … a metà. Aver trovato la composizione relativistica delle velocità, solo in un caso estremamente particolare (anche se è quello che ci serve per il diagramma di Minkowski), gli stava stretto. Accontentiamolo con questa aggiunta più generale. In fondo non è poi molto complicata…

