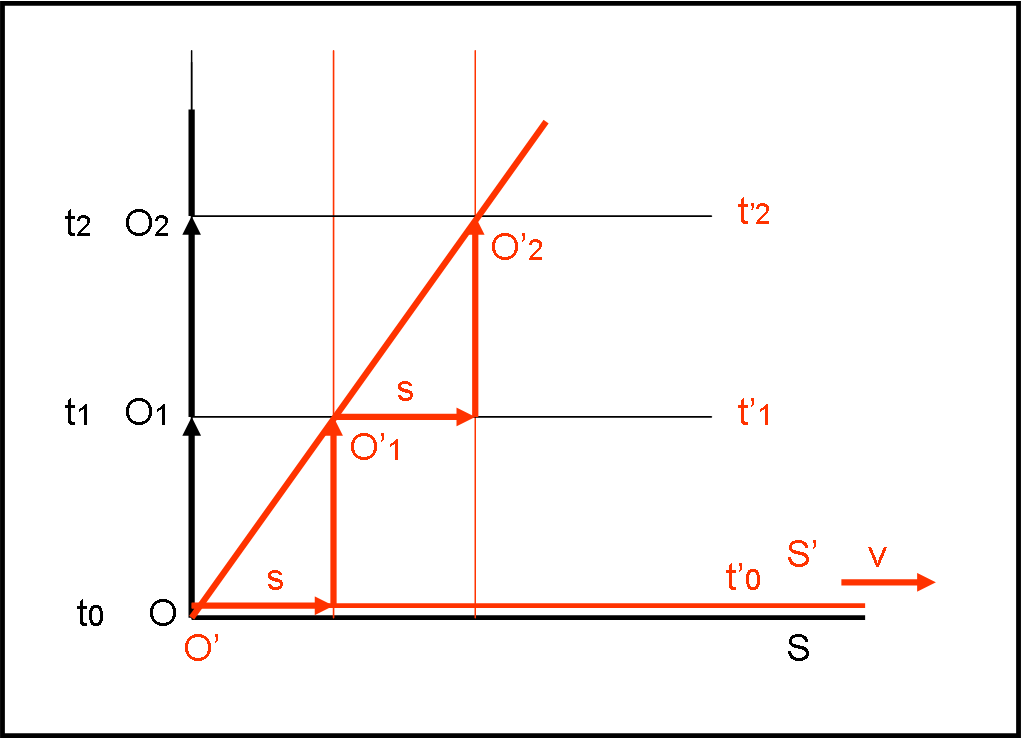
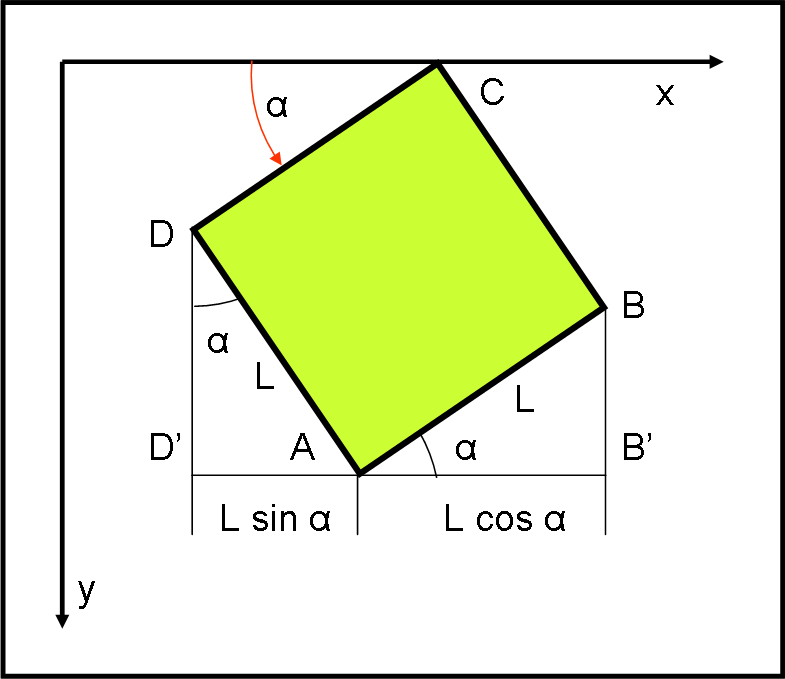
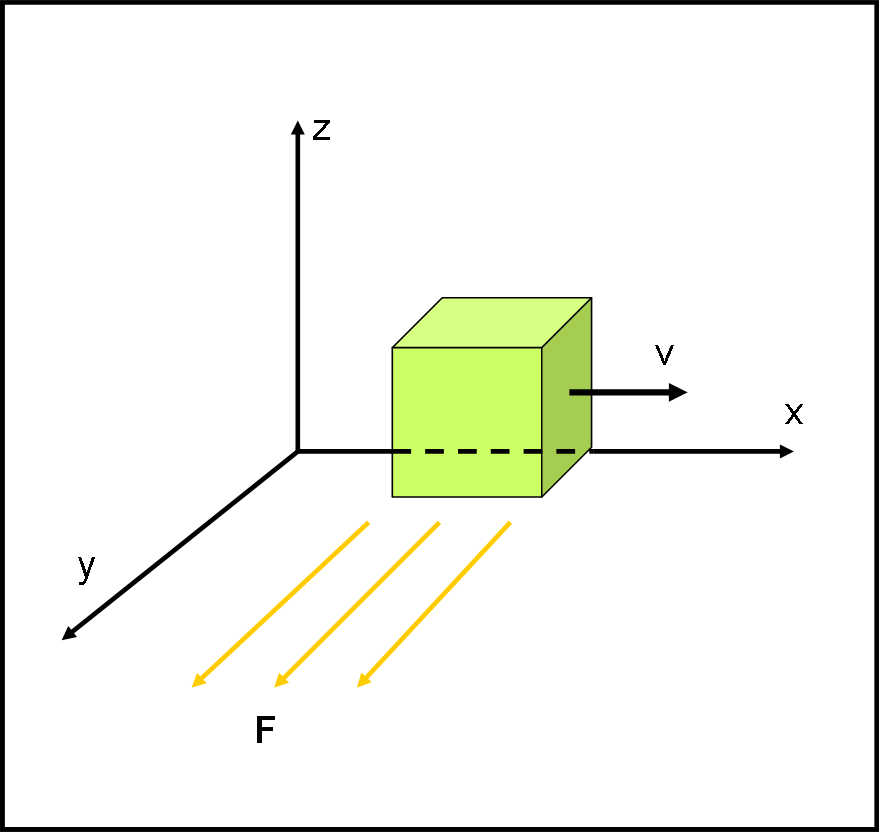
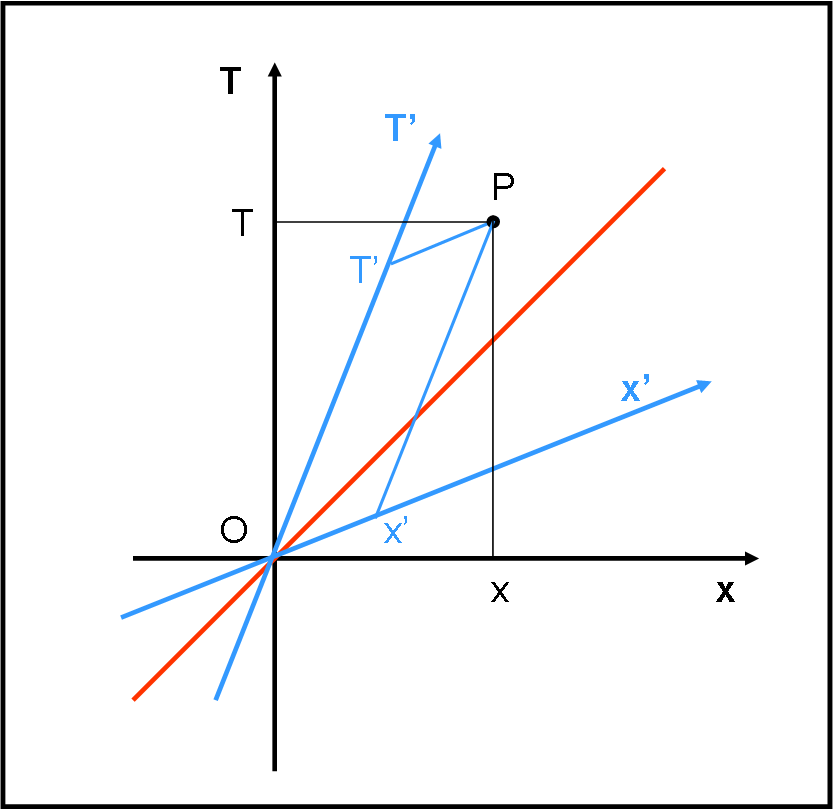
Innanzitutto, devo chiedere scusa a SuperMagoAlex, mio insostituibile amico-collega-assistente. Tra pochi giorni terrà una conferenza a un pubblico di astrofili e appassionati sul concetto di “tempo” o giù di lì. Un’impresa non facile che lo sta occupando a "tempo" (quasi) pieno. Mi ha chiesto personalmente di non inserire nuovi quiz che lo distrarrebbero… Però, però, Lorentz mi ha contattato, mi ha “bacchettato” e devo intervenire. Inserisco, quindi, un nuovo quiz analogo a quello precedente. Tuttavia, non darò la risposta fino a quando SMA non avrà avuto il tempo di dedicargli un po’ di tempo (più o meno una settimana). L’attesa avrà come premio la pubblicazione, sul sito del nostro “circolo”, dell’intera conferenza. Forza SMA siamo tutti con te! Gli altri, intanto, facciano un po’ di ripasso e qualche piccola operazione matematica. Come vedete, il quiz ha solo due asterischi e quindi è veramente facile…