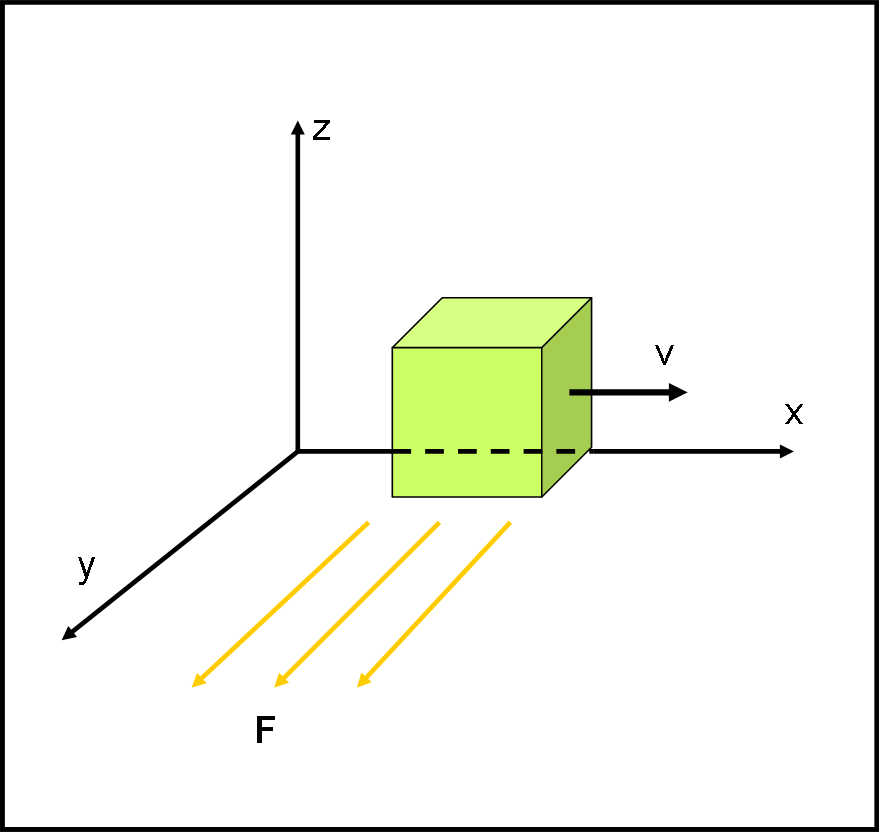
Questo articolo è la risposta all’ultimo quiz sulla composizione delle velocità nell’ambito della relatività ristretta. Sarà mia cura inserirlo, in seguito, alla fine dell’articolone generale sulla RR che è ora in evidenza. Dovrò anche rimettere a posto le parti sul diagramma di Minkowski e proseguire con qualche altro concetto fondamentale. Sicuramente, ho fatto un po’ di caos, saltellando di qua e di là e tornando indietro ad approfondire qualche parte più ostica. Prometto che alla fine tutto sarà esposto con maggiore logica e ordine. Chi vuole ancora cimentarsi con il quiz… non legga questo articolo. Per andare avanti basta fare proprio il risultato finale.
Volevo scrivere un articolo su questo problema estremamente importante della RR. Poi ho pensato che qualcuno di voi potrebbe essere in grado di risolverlo da solo e allora lo inserisco come quiz di pura matematica. Esso ha bisogno solo della trasformazione di Lorentz… In seguito inserirò la soluzione come articolo facente parte della RR.
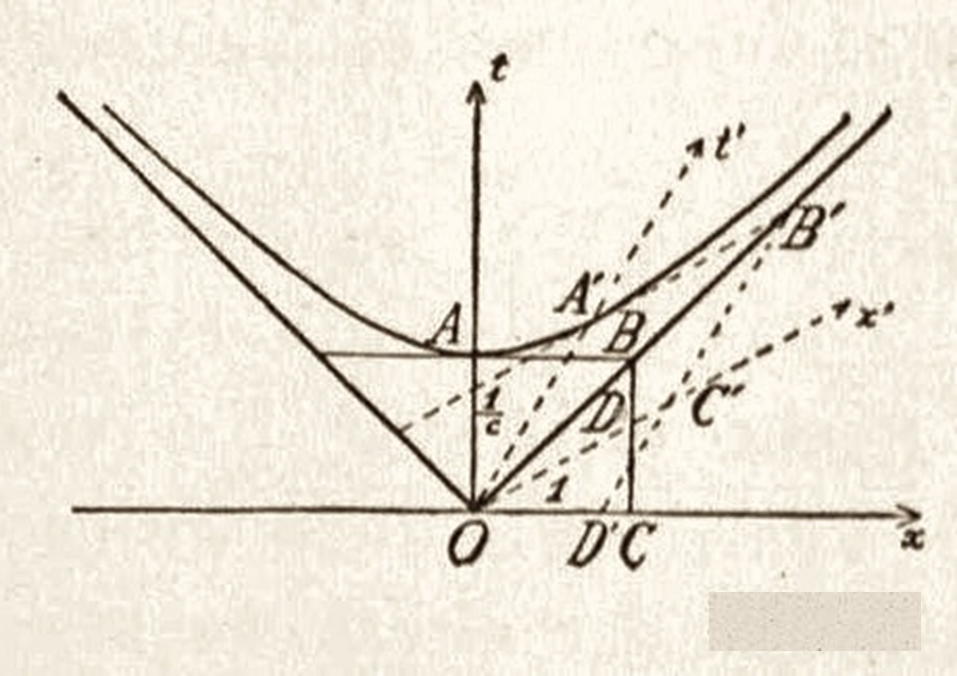
Questo quarto articolo conclude in qualche modo la presentazione del diagramma di Minkowski da un punto di vista puramente geometrico. Viene introdotto l’invariante spaziotemporale e si capisce molto meglio cosa rappresentano le iperboli trovate precedentemente. La dilatazione dei tempi segue quasi automaticamente. Tuttavia, ci fermiamo un attimo prima. L’articolo può risultare un po’ difficile se non si legge con grande attenzione e non si collega continuamente con quelli precedenti. Lo lasciamo un bel po’ in visione in attesa di domande e dubbi riguardanti “solo” lui. Mi raccomando, non cerchiamo di estrapolare in avanti se no si rischia veramente di confondere i meno preparati. Lo scopo ultimo deve essere quello di regalare a TUTTI la RR e non provare la capacità di pochi…
Grazie a Daniela, aggiungo poche parole per spiegare ancora meglio come si debbano interpretare i sistemi di riferimento nella RR (ma non solo…). Vedete quanto sono importanti i dubbi e le domande? Mi permettono di capire i punti più critici che, magari, mi sono sfuggiti a una prima descrizione.
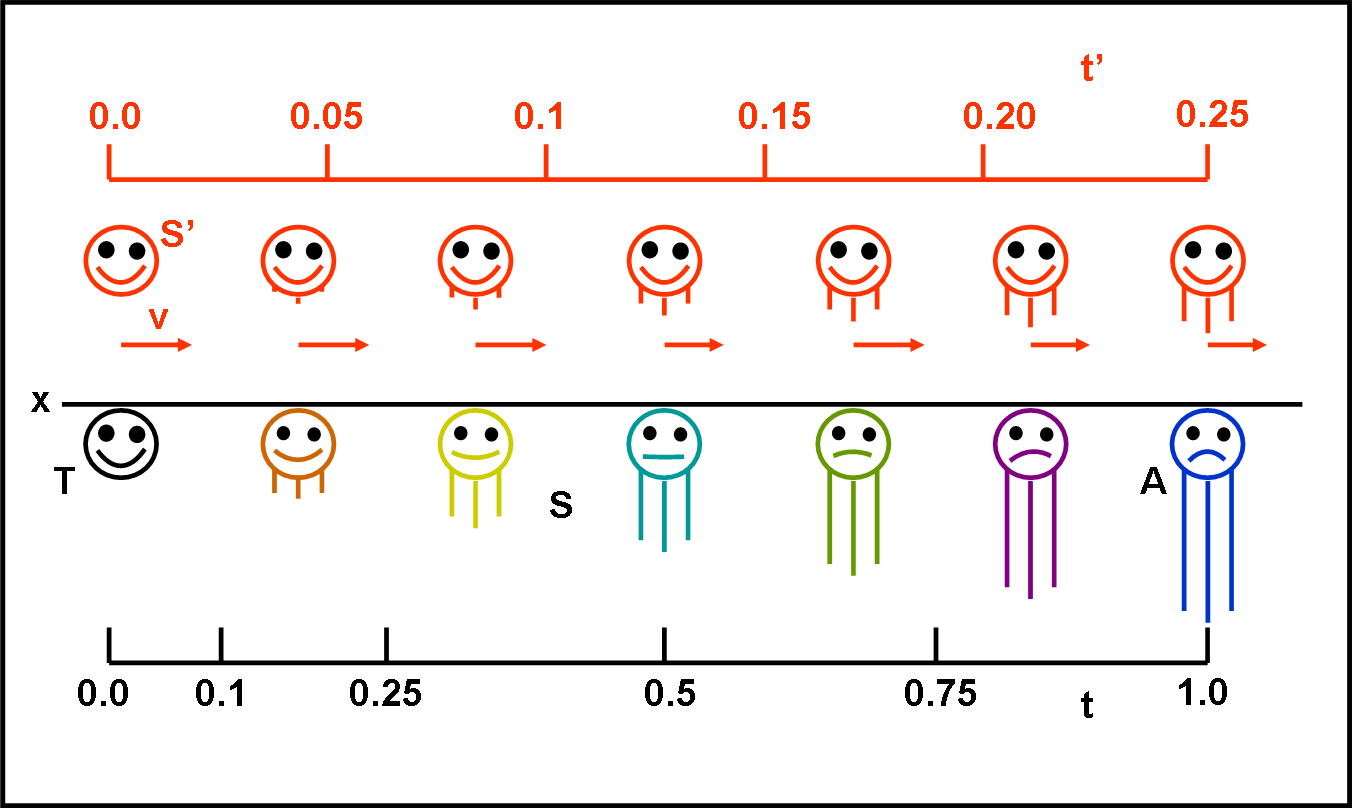
In attesa di proseguire con il diagramma di Minkowski, divertiamoci a impostare il paradosso dei gemelli che ci verrà molto utile per controllare se abbiamo compreso esattamente ciò che realmente capita quando si osserva un sistema in movimento. Proviamo a definirlo in modo molto semplificato, evidenziando alcuni punti che spesso non sono spiegati esaurientemente. Un piccolo esercizio senza pretese, ma che può chiarire molti dubbi e confusioni.
Al di là dei possibili articoli di ulteriore chiarimento di problematiche particolari, cerchiamo di fare il punto dei concetti principali che vanno fatti propri prima di proseguire con la RR e la sua rappresentazione in un “semplice” diagramma bidimensionale. Spero che possa essere d’aiuto per chi sta leggendo o ha già letto la RR, messa in evidenza.
Completiamo l’ennesima descrizione di come si possa dimostrare in modo molto semplice la relatività della simultaneità. Ogni sistema di riferimento, in moto relativo rispetto a un altro, ha una sua linea di simultaneità. Questa conclusione segue direttamente dalle ipotesi di Einstein ed è la base di tutta la RR.
Non mi picchiate, ma approfitto di un attimo di tranquillità per cercare di semplificare ancora di più la descrizione di simultaneità relativa. In questa prima parte dico cose che sono ridicole per chi ha già capito il problema (ma una lettura potrebbe confermare del tutto la comprensione). Gli altri, che hanno ancora dei dubbi, lo leggano attentamente e mi dicano subito se trovano qualche concetto non chiarissimo. Dobbiamo rendere sempre più solide le basi! Vi chiedo, però, di non estrapolare o cercare di vedere oltre. Ogni cosa a suo tempo. Per adesso, mi basta capire ciò che avete veramente… capito.
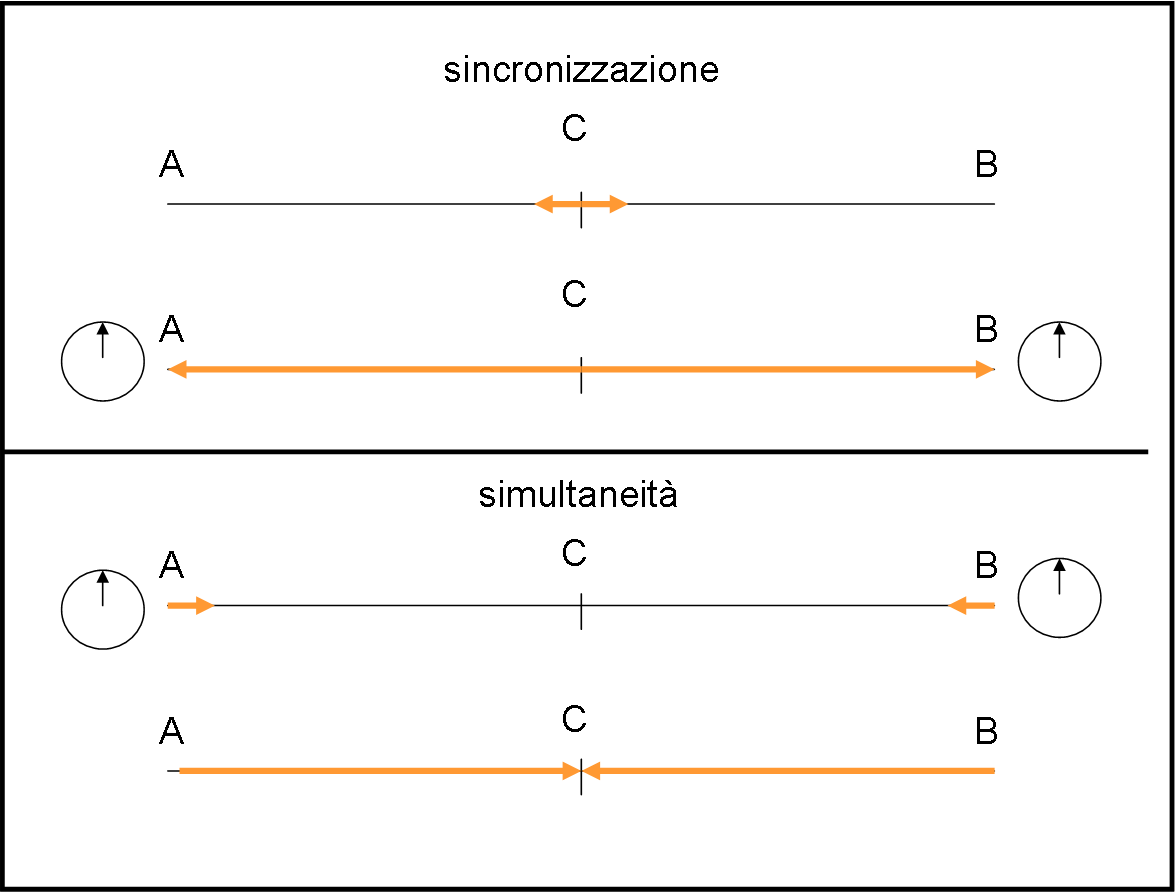
Affrontiamo nuovamente la simultaneità di due eventi e la sua relatività rispetto a due sistemi inerziali in moto relativo. Lo facciamo in modo ultra semplice e qualitativo, ma, passo dopo passo, arriviamo quasi automaticamente a rappresentare il concetto di base, quantitativamente, sul diagramma di Minkowski. Concludiamo con un piccolo “test” di verifica.
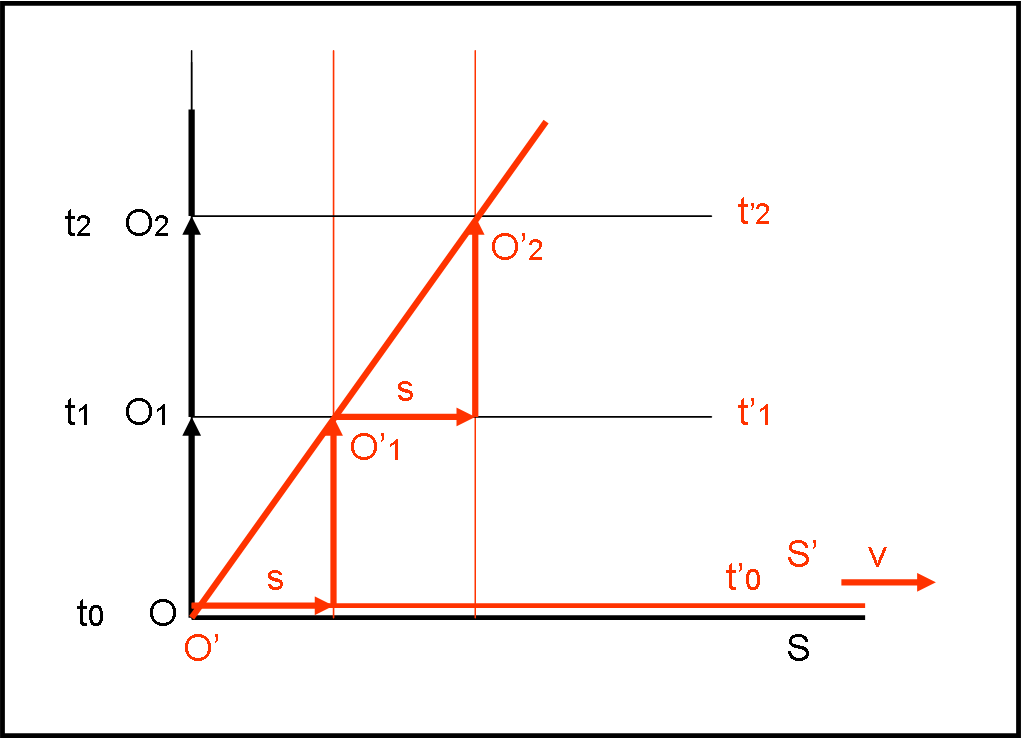
Secondo appuntamento con la RRR, forse addirittura ancora più banale e ripetitivo del primo. Tuttavia, alcuni concetti importantissimi si fanno già strada tra tante ovvietà. Uno fra tutti è la necessità di usare due orologi per misurare "qualcosa" su un altro sistema.
Iniziamo ad approfondire, semplificando al massimo (spero), alcuni concetti base della RR. Lo facciamo anche con quelli più ovvi e banali (apparentemente). Bloccatemi appena qualcosa non appare completamente logico o intuitivo. Questo articolo è un tentativo per capire, tutti assieme, se è utile oppure no rivedere i concetti essenziali. Nel caso, aggiungeremo qualche parte nella trattazione della RR complessiva. Forza, lavoriamo insieme per costruirci la nostra RRR. Vi prego, però, di esprimere i vostri dubbi. Nessun commento significa comprensione totale. Intervenire dopo aver introdotto molti altri concetti renderebbe la faccenda sempre più caotica e confusionaria.
Questo articolo vuole solo essere una esercizio per mettere alla prova la comprensione dei concetti che abbiamo descritto finora. E’, quindi, un invito a passare all’azione e controllare se avete digerito la logica descritta finora. Completato l’esercizio, ci fermeremo a osservare i risultati ottenuti e cercheremo di capire la loro “stravaganza”. Questa riflessione servirà come punto di partenza per una trattazione molto più tecnica e generale.
La Relatività Speciale o Ristretta, insieme alla sua rappresentazione completa nel diagramma di Minkowski, sono troppo utili, importanti e affascinanti per non essere digerite perfettamente e senza ripensamenti o dubbi. Penso che sia più utile fermarci un po' e rileggere attentamente quanto scritto finora e cercare di dipanare tutti i dubbi. Questo "post" potrebbe raccogliere idee, commenti, dubbi, incomprensioni e tutto ciò che vi salta in mente... Poi, potremo entrare nello spazio non euclideo di Minkowski molto più sereni!
Continuiamo a prendere conoscenza con il diagramma di Minkowski. Abbiamo visto che la trasformazione di Lorentz trasforma un sistema di assi ortogonali in un sistema di assi non ortogonali. Per definire il nuovo sistema è, però, necessario ricavare l’unità di misura sui nuovi assi ottenuti con la trasformazione.
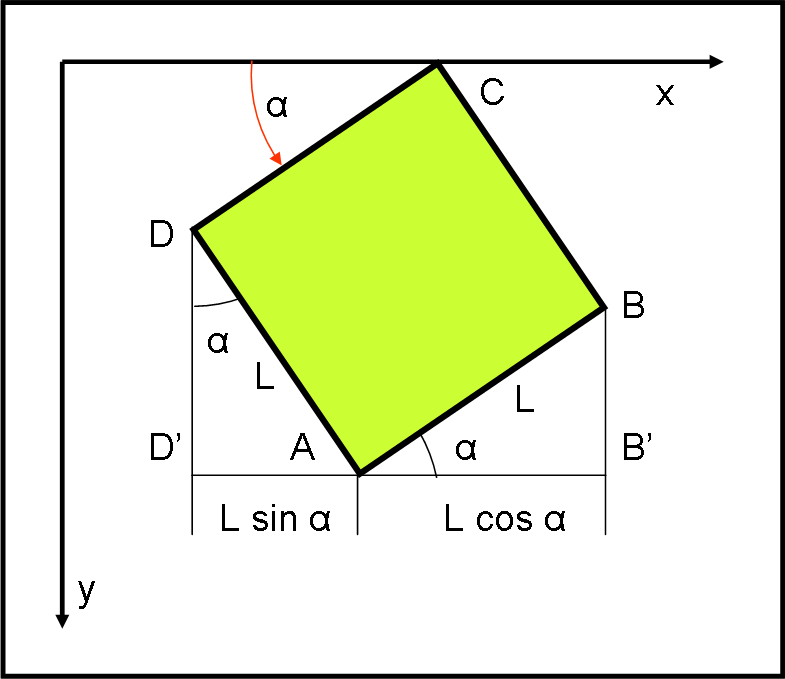
Questo articolo (che fa parte della relatività speciale) è anche la soluzione del quiz sulla contrazione di Lorentz che non si vede ma… c’è. Esso può essere spiegato, in prima approssimazione, con una geometria molto semplice e immediata. Per non smentirci mai, alla fine viene prospettato un nuovo esercizio di analisi matematica…