Affrontiamo una delle parti più ostiche, facendola, però, seguire da alcune considerazioni e riflessioni molto più semplici.
Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.
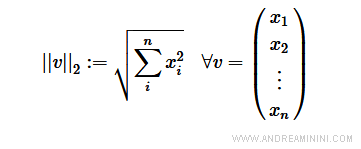
Una breve precisazione che tornerà utile nel prosieguo dell'analisi della relatività generale...
Facendo viaggiare un vettore su una superficie sferica si può definirne la curvatura.
Sembra impossibile, ma l'energia del fotone è ancora qualcosa che crea dubbi e confusione in tante persone (ovviamente, parlo solo di quelli che desiderano sapere e non della grande massa). Ne abbiamo già parlato in lungo e in largo, cambiando il modo di vedere le cose, ma aggiungere qualcosa fa sempre bene, dato che potrebbe far scattare la molla finale. Questa volta ne do una versione molto particolare che se da un lato semplifica, dall'altro potrebbe aiutare a comprendere.
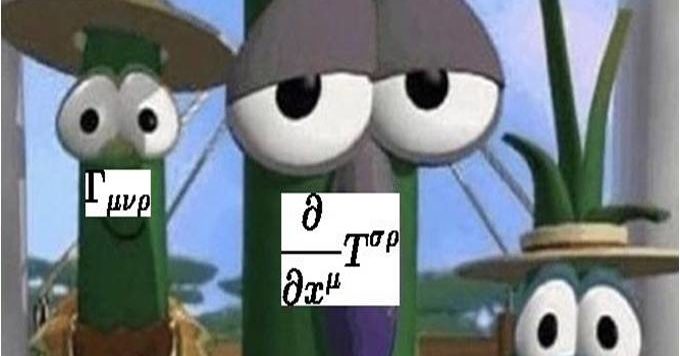
Questa parte è decisamente molto ostica e non tutto può essere ricavato nei limiti imposti al Circolo. Malgrado si debba prendere per buona una certa dimostrazione, la trattazione ha dei risvolti non banali, al limite della professionalità. Di meglio non riesco a fare...
In questo articolo propongo alcuni degli argomenti affrontati da Enzo nel 6° articolo della serie “La relatività Generale al microscopio” applicati al caso particolare delle coordinate cartesiane e coordinate polari nello spazio Euclideo. L'obiettivo è di illustrare tramite queste due coordinate il percorso che porta al tensore metrico o metrica.
Partendo dal teorema di Pitagora sul piano arriviamo a quello su uno spazio curvo, grazie al tensore metrico... le cose si complicano e le sommatorie si affollano.
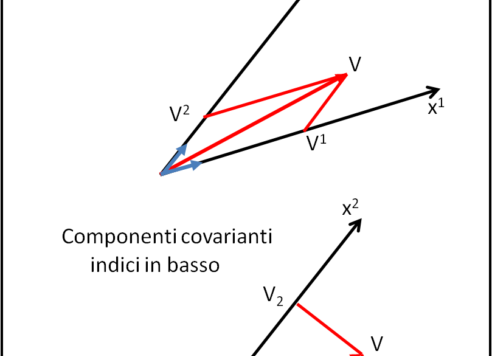
E' ora di trasformare i tensori e di introdurre, in modo estremamente didattico, le coordinate controvarianti e covarianti. Le cose si complicano un poco e devo limitarmi a dare alcune definizioni ...
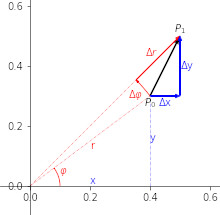
La domanda 2 del precedente articolo è un poco più difficile delle altre poiché richiede il calcolo di alcune derivate non banali.
Descrivo qui i passaggi in modo che chi li ha portati a termine possa confrontare la soluzione trovata e chi non è riuscito ad arrivare in fondo possa avere un aiuto.
In questo articolo propongo alcune domande ed alcuni approfondimenti sulle trasformazioni dei vettori trattate nell'articolo La Relatività Generale al microscopio. 4: I Tensori **. Cerco anche di collegare i vettori e le loro trasformazioni con le entità trattate negli articoli precedenti. In particolare scalari (tensori di rango 0) e gradienti.
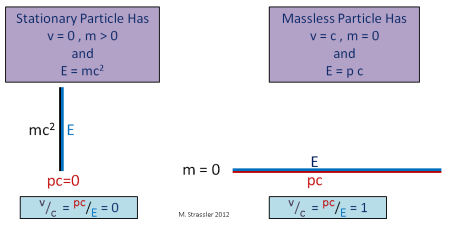
Un piccolo appunto di dinamica relativistica per rispondere coralmente a una domanda che mi è stata fatta varie volte. Ne abbiamo già parlato, ma non è mai ripetitivo ribadire i concetti essenziali della relatività
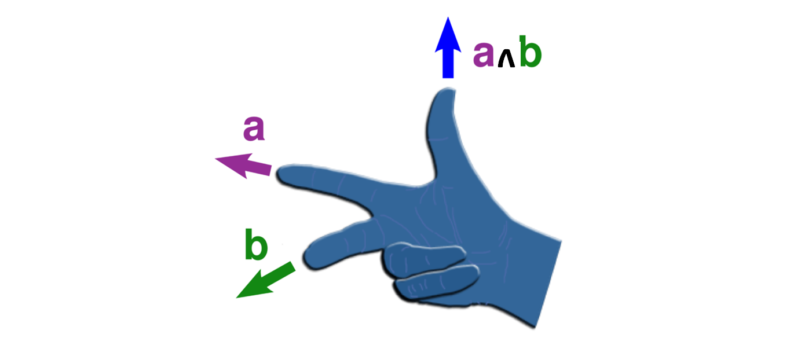
Introduciamo nuovamente i tensori, tenendo ben presente che abbiamo lavorato tanto per riuscire a manipolare correttamente le loro coordinate, cambiando sistema di riferimento. Ci aspetta un bel ... "lavoro"!
Questo articolo fa parte della sezione "METTIAMOCI ALLA PROVA!" all'nterno della Relatività Generale al microscopio Seguendo gli articoli di Enzo della serie La Relatività Generale al microscopio ho cercato di mettermi alla prova applicando le nozioni illustrate a qualche caso particolare. Ho pensato che poteva essere interessante anche per altri frequentatori del circolo confrontarsi con […]
Un'idea di Fabrizio veramente grandiosa che mi dà un aiuto enorme sia pratico che morale. Grazie!
Abbiamo definito il valore di un "campo" in un certo sistema di riferimento. Questo valore deve, però, non dipendere dal sistema usato e perciò è necessario imparare a trasformare le coordinate di un sistema in quelle di un altro sistema. Facciamo il primo passo in tal senso.