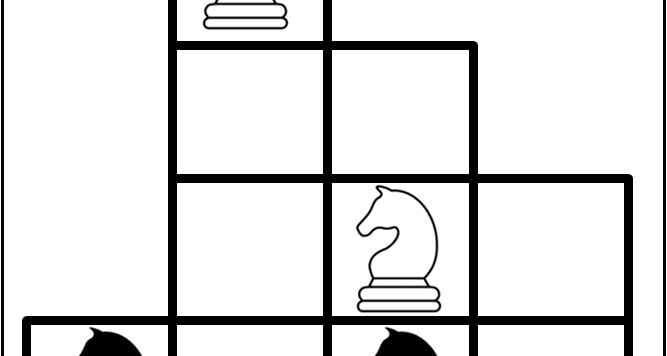
Quest'articolo nasce su richiesta di Enzo, affinché si possa descrivere in maniera chiara e comprensibile la soluzione del quiz . Vi è una porzione di scacchiera, costituita da 10 caselle, sulla quale sono collocati 4 cavalli, 2 bianchi e 2 neri, disposti secondo l’ordine schematizzato nella figura seguente: Posizioni iniziali dei cavalli Il movimento di […]