Un quiz piuttosto semplice che potrebbe essere risolto anche dai meno esperti... chissà mai?! Comunque, un invito per passare le ferie su Papalla e visitare Matlandia.


Un quiz piuttosto semplice che potrebbe essere risolto anche dai meno esperti... chissà mai?! Comunque, un invito per passare le ferie su Papalla e visitare Matlandia.
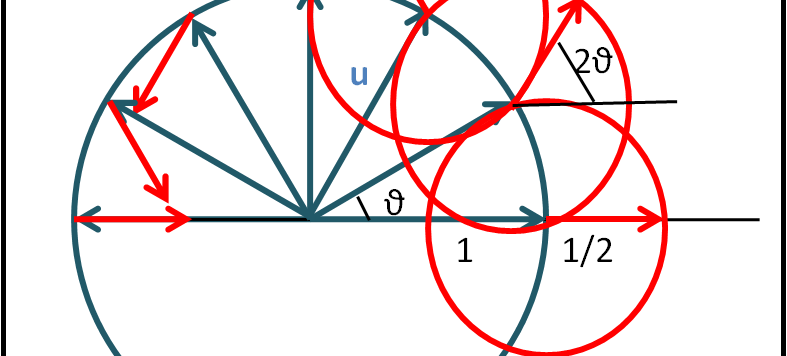
Prendiamoci un attimo di respiro e mostriamo una simpatica (e utile) visualizzazione della serie di Fourier tramite la rotazione di più vettori.

Due studentesse liceali (dal colore scuro della pelle, ma dal cervello decisamente chiaro e limpido) hanno risolto un problema su cui hanno lavorato per secoli i grandi matematici. Abbiamo di fronte una vera opera d'arte matematica!
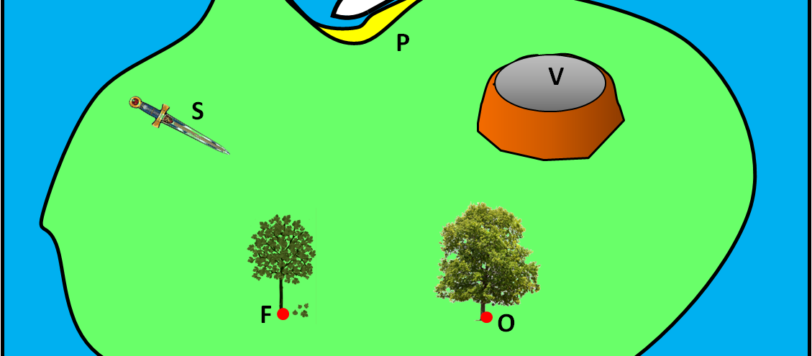
Un quiz simpaticissimo (almeno secondo me) e molto istruttivo. Sembrerebbe praticamente impossibile (quattro asterischi), ma in realtà la soluzione è veramente semplice (un asterisco). Buon divertimento e non abbiate paura del pirata!

Dopo tutti gli sforzi di Mau, un piccolo-grande aiuto per svegliare anche i ... sonnolenti!
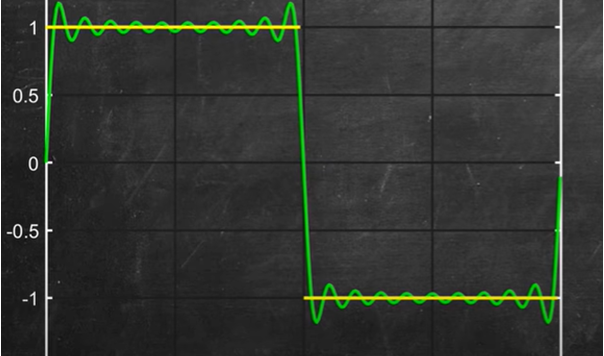
E' venuto il momento di fare un'applicazione "concreta" della serie, ma il discorso non è ancora finito...

Forse ci sono vari metodi per risolvere questo quiz, non certo troppo difficile. Spero che venga fuori la brillante soluzione di Arogatip...
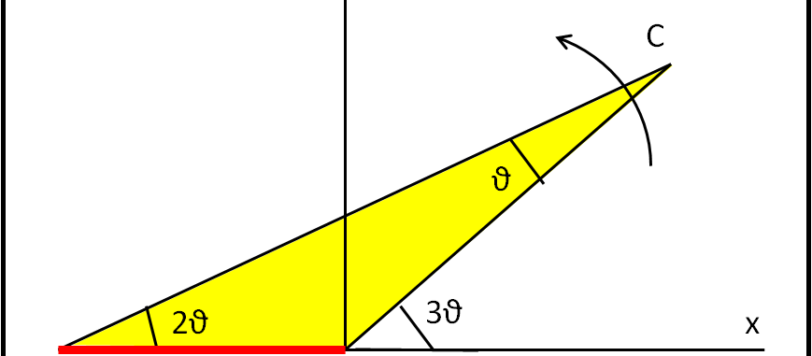
Grande partecipazione per questo quiz non banale. Grazie ai nostri Andy, Fabrizio, Leandro e Maurizio che hanno giocato a generalizzare il problema.

Introduciamo la serie di Fourier e, in particolare, ne calcoliamo i coefficienti. Leggetela con calma perché è piuttosto faticosa...

Limitiamoci a quiz piuttosto impegnativi, che, finora, hanno avuto un buon seguito. Poi vedremo...
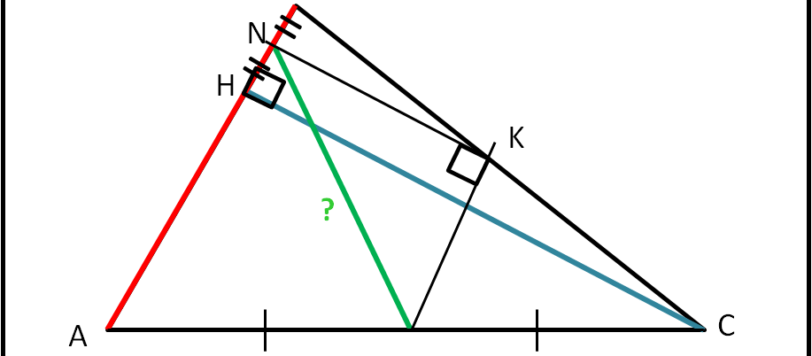
Innanzitutto, grazie a Paolo che non ha avuto timore a cimentarsi nel quiz. Ha dato la soluzione per un caso particolare che, comunque, è anche valida per un triangolo qualsiasi. Per trovare velocemente la soluzione basta ricordare una delle proprietà del triangolo che ho inserito in un articolo posteriore (anch'esso in attesa di risposte...). In […]