Sembra impossibile, ma di barcaioli ve ne è sempre bisogno, anche nel XXI secolo!
Completiamo la serie di articoli sui limiti notevoli e sulle derivate fondamentali. Spero, come sempre, che Albertone evidenzi gli errori di scrittura, quasi sicuri in questo periodo....
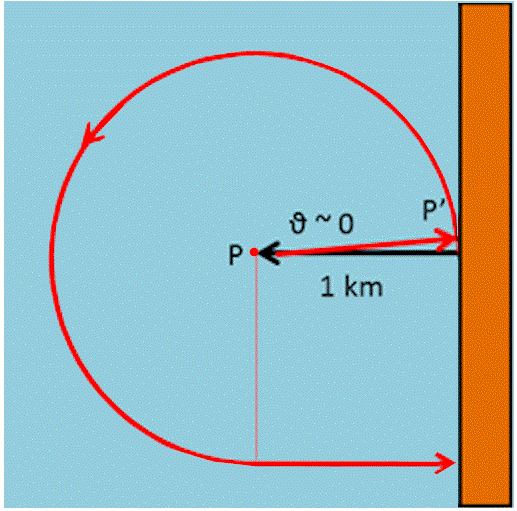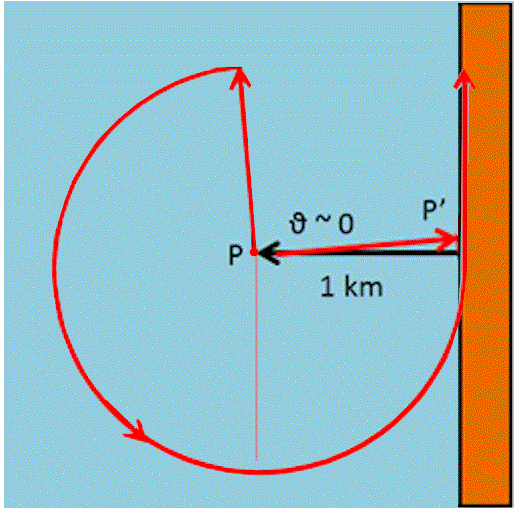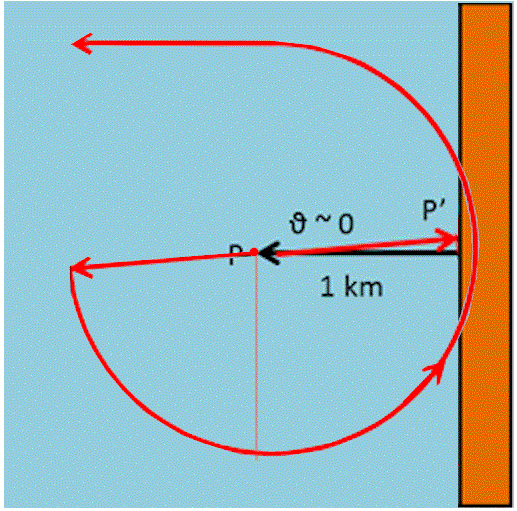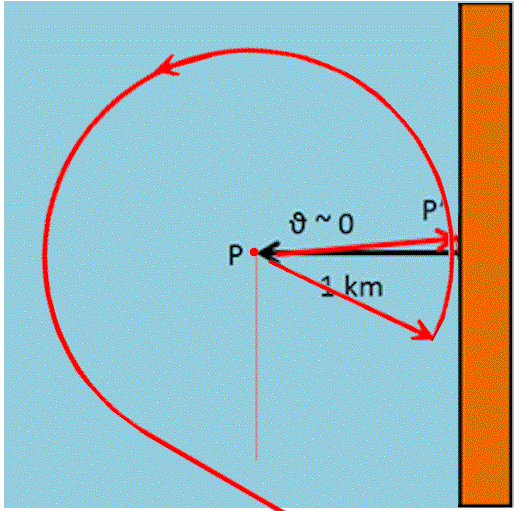
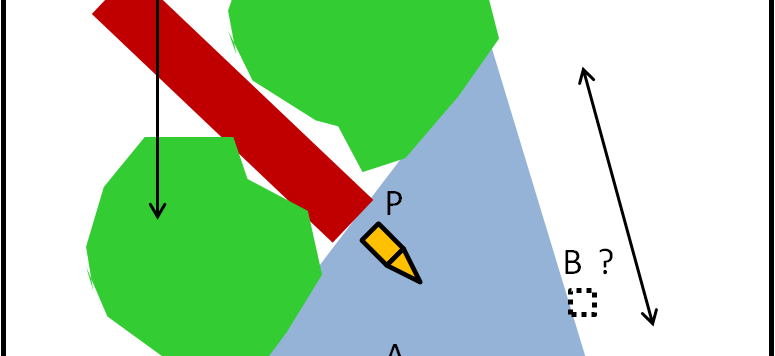
Siete in mare, lontano dalla costa e improvvisamente cala una nebbia fittissima... Un po' di semplice trigonometria vi può salvare la vita!
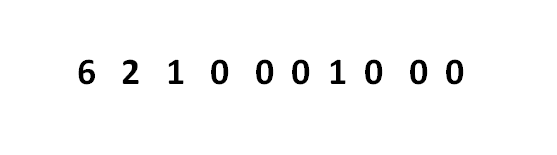
Andy e Maurizio si sono scatenati arrivando rapidamente alla soluzione e andando ben oltre. Io riposto, modestamente, solo l'indispensabile per entrare nella stanza...
Per risolvere il mistero riguardante l'ultimo teorema di Fermat, Pippo deve riuscire ad aprire una stanza segreta dove è contenuto un manoscritto del grande, ma un po' strano, matematico francese. Riuscite ad aiutarlo? Poca matematica e tanta logica...
Maurizio è stato velocissimo nello "scardinare" il problema. Io riporto la via forse più semplice, passando ancora una volta alle tre dimensioni.
La soluzione non era difficile e non unica. I meno esperti, però, sono stati silenti. Torniamo, quindi, a problemi un po' meno banali...
In attesa di un nuovo quiz piuttosto difficile, eccone uno per i meno esperti... Invito i più bravi ad aspettare un paio di giorni. N.B.: Il quiz è stato aggiornato, imponendo il non piegamento del foglio.
Geometria applicata a una pizza? Sì, ma senza esagerare.
Calcoliamo tre limite notevoli che ci saranno utili per il calcolo di altre derivate. Per far ciò dobbiamo ricordare il limite che definisce il numero di Nepero e.
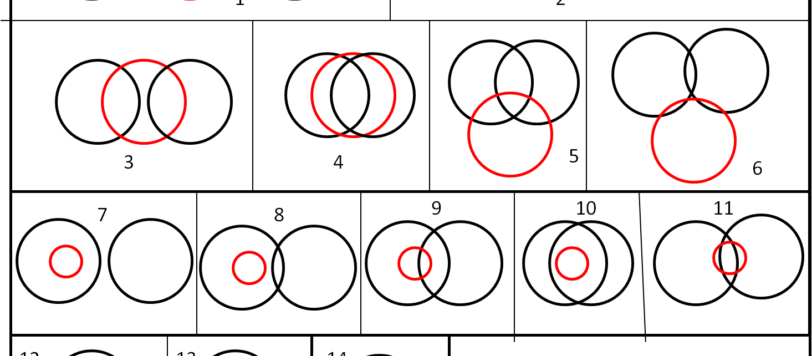
E' stato risolto il problema relativo a tre cerchi. Riportiamo la soluzione, aspettando qualche possibile passo in più verso i 4 e i 5 cerchi...
Il problema dei tre cerchi ha interessato molto... perché, allora, non continuare con un gioco geometrico?
Ecco la soluzione di un problema che ha interessato svariati lettori "matematici" e che ha mostrato varie soluzioni. La parte di Arturo deve essere ancora completata e l'abbiamo trattata rapidamente.
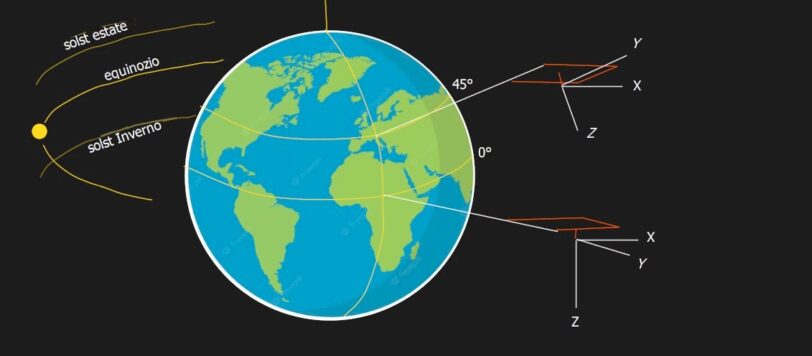
Le matrici di rotazione possono trovano una originale applicazione nel tracciamento delle curve di una meridiana.
Completiamo la parte trigonometrica con un paio di ulteriori limiti notevoli.
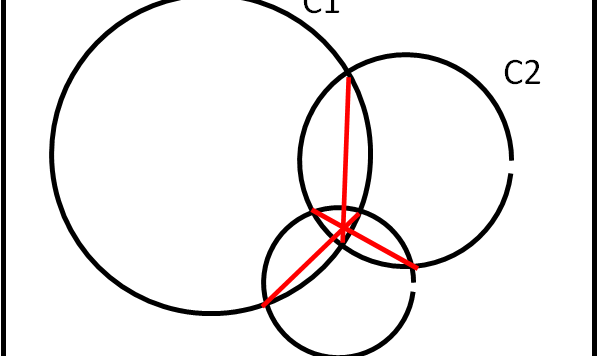
Voglio presentarvi un simpatico problema piano legato alla convivenza di tre cerchi qualsiasi, che si intersecano vicendevolmente. Lo presento come "quiz", ma vedremo che servirà a introdurre due nuove definizioni e aprirà la strada a interessanti casi particolari. Insomma, tre cerchi ne possono "combinare" delle belle...