Questo articolo si propone di fornire un semplice strumento per rappresentare il meccanismo della rotazione in forma vettoriale, scomponendo e semplificando il problema di determinare i cambiamenti di orientamento dovuti a spostamenti rotatori.
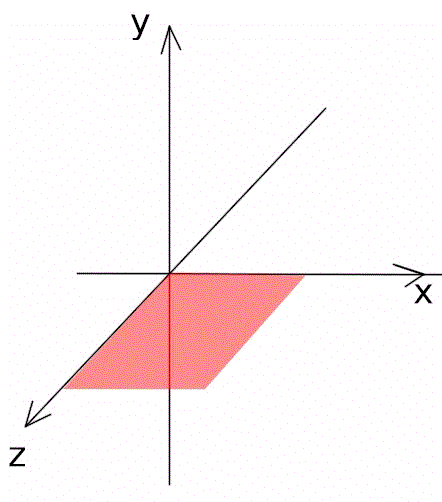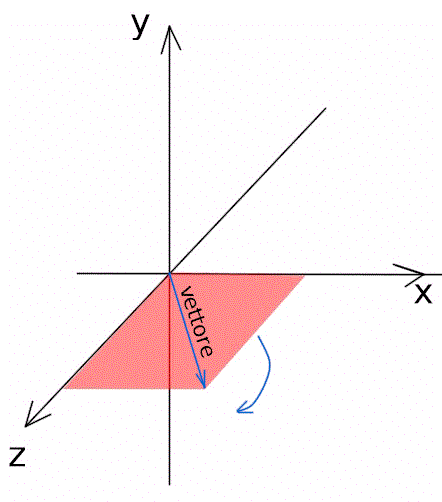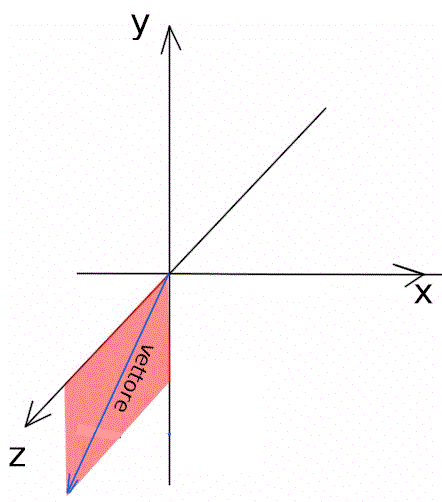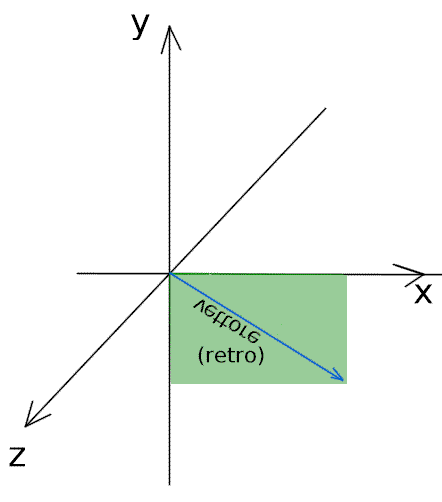

Questo articolo si propone di fornire un semplice strumento per rappresentare il meccanismo della rotazione in forma vettoriale, scomponendo e semplificando il problema di determinare i cambiamenti di orientamento dovuti a spostamenti rotatori.

Una soluzione tecnologica di estrema semplicità ha permesso di far correre i treni su due stretti binari senza farli deragliare, soprattutto in curva. Vediamo di descriverla in modo puramente geometrico.
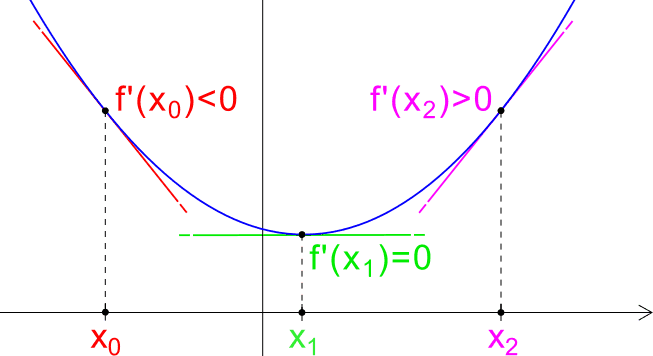
Quando avevo scritto il corso di matematica avevo riportato solo le derivate delle funzioni fondamentali, evitando di dimostrare come potevano essere ottenute. Direi che è giunto il momento di farlo, dato che il Circolo e i suoi lettori sono ormai "maturi". Ringrazio, in particolare Albertone, che mi ha stimolato a fare questo passo. Consideriamola un'aggiunta alle lezioni di matematica...
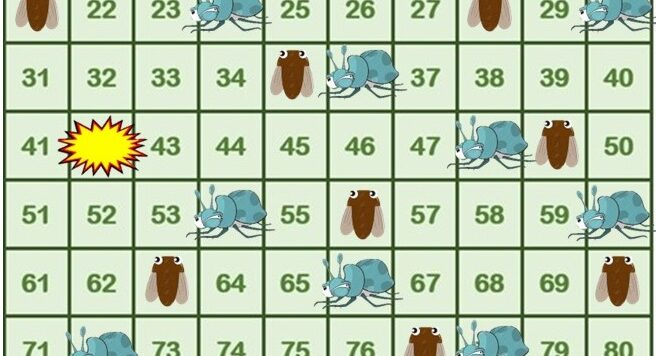
Nelle foreste del nord America alcuni generi di cicala vivono nel sottosuolo per 17 o 13 anni, per poi emergerne, tutte insieme, nell’arco di una notte. Perché ciò accada non lo sappiamo. In questo articolo illustriamo una possibile spiegazione di natura matematica e, per non farci mancare niente, proponiamo un’alternativa al classico gioco dell’oca per introdurre i più piccoli (ma anche i più grandi) al magico mondo dei numeri primi.

Oggi, 23 novembre, è la giornata mondiale dedicata a Fibonacci e ci uniamo alle celebrazioni riproponendo la tesina che la nostra Valentina scrisse nel 2018 per il suo esame di maturità.
Un quiz che è, forse, risultato un più difficile del previsto. Bravo, come sempre, al nostro Fabrizio.
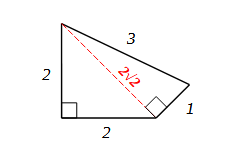
Questo articolo nasce come una serie di considerazioni e prove numeriche “sul campo” relative al teorema di Pitagora e all’ipotesi di Enzo su di una sua estensione a qualsiasi poligono, che ha ottenuto un primo riscontro particolare grazie alla “riscoperta” della spirale di Teodoro di Cirene. L’ipotesi di Enzo era quella di vedere, se possibile, l’applicabilità del teorema di Pitagora anche a poligoni con più di tre lati. Così ho deciso di tentare algebricamente se fosse stato possibile trovare una identità di tipo pitagorico (inizialmente limitata solo per valori interi) per poligoni generici con più di tre lati.