Un quiz che ci rimanda ancora una volta alle costruzioni con riga e compasso e al grande Gauss.
Bravissimo Dario che "distrugge" il puzzle!
Due costruzioni dell'ellissi sembrano del tutto scorrelate e, invece...
Un aiuto per la soluzione...
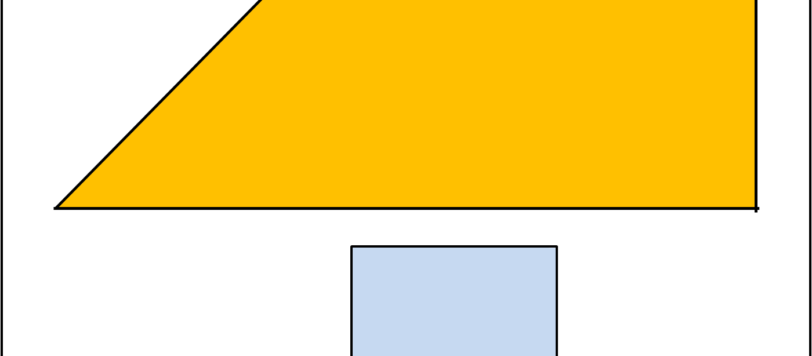
un puzzle con solo due pezzi, ma tutt'altro che banale, anche se può essere risolto da chiunque abbia un po' di fantasia.
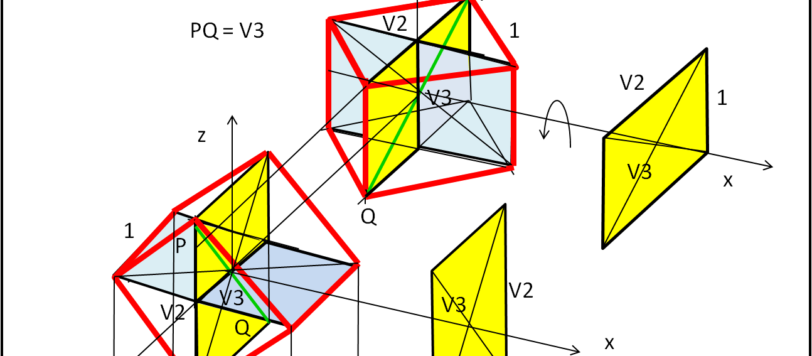
Una soluzione piuttosto lunga, ma che spero sia pienamente comprensibile... Come al solito... grande Andy!
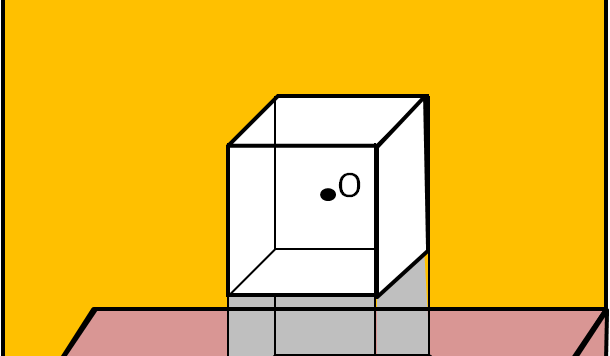
Un problema che sembrerebbe abbastanza banale ma che riserva delle difficoltà inaspettate. Oltretutto, è quasi impossibile trovarlo sul web.
Un articolo che riempie una lacuna e che forse fa contento Alberto
Ottime risposte per un problemino che ha sollevato non poche discussioni anche tra matematici e fisici...
Un quiz apparentemente molto facile, ma...
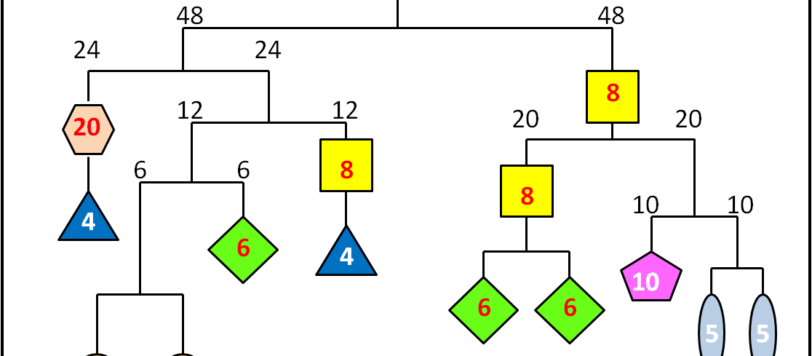
Una soluzione di puro ragionamento, ribadendo, però, che la formulazione matematica di Francesco è perfetta.
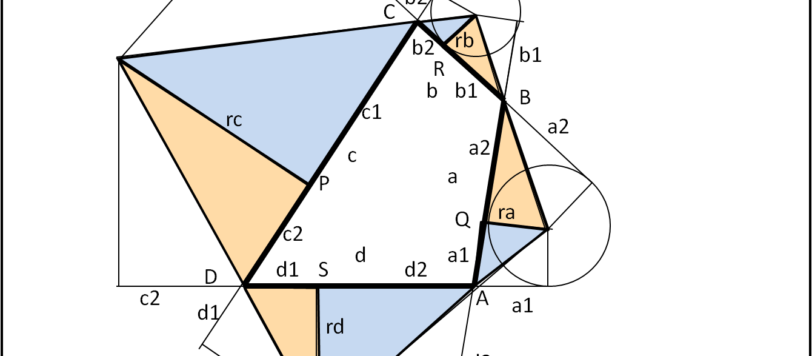
Concludiamo la dimostrazione della formula di Brahmagupta, con molta pazienza e attenzione...
Un interessante esercizio dedicato alle potenze di potenze...
Una risposta immediata ad Alberto... sperando che per un po' si accontenti!
L'astrofisica di punta latita e, allora, cerchiamo di divertirci con la matematica. Partecipiamo anche noi alle Olimpiadi e ci accorgeremo che sono necessarie soprattutto fantasia e logica, unite solo e soltanto alle basi più semplici dell'algebra e della geometria.
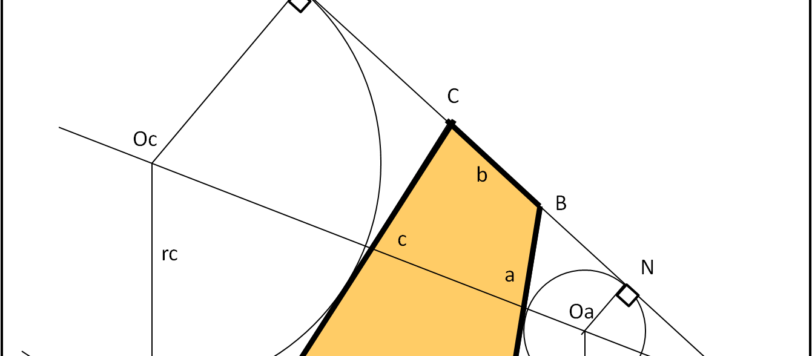
Non spaventatevi dei quattro asterischi... Essi non sono dovuti a calcoli complessi o a nozioni che sono bagaglio di pochi. Tutta la dimostrazione si basa su una geometria veramente semplice così come è elementare quel po' di matematica che la condisce. Il vero problema è scovare le giuste relazioni tra le grandezze in gioco. Un modo divertente per dare il giusto rilievo a un grande matematico indiano, Brahmagupta. Il nostro Leandro, vero mago matematico, conosceva la formula e, magari, potrebbe anche trovare un metodo alternativo di dimostrazione.