Un quiz introduttivo...
un facile quiz molto estivo...
Dal pentagramma all'uovo e alla sua equazione...
Resta un dubbio: è meglio un buon matematico o un pistolero saggio?
Per qualche dollaro in più, ossia come sanare senza rimetterci una lite familiare.
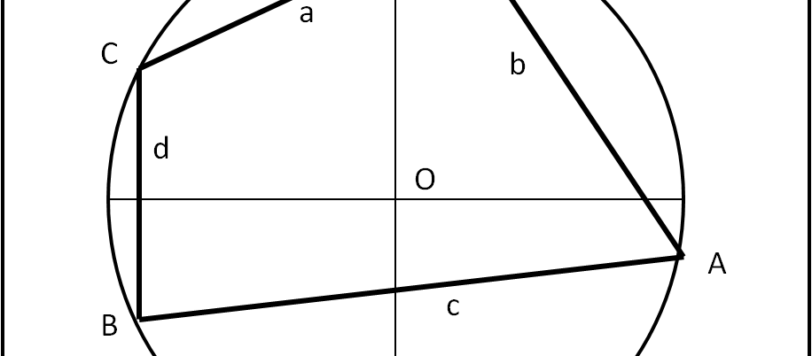
Lewis Carroll, l'autore dello straordinario romanzo "Alice nel Paese delle Meraviglie", sapeva anche costruire interessanti quiz relativi alle probabilità. Un anticipatore di Bertrand ?
Il paradosso di Bertrand è stato risolto (forse), ma che fatica!
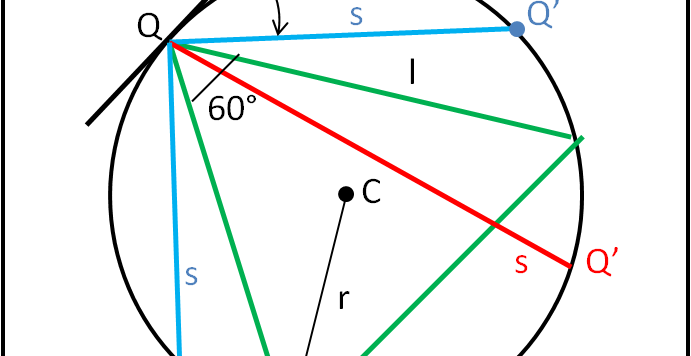
Un classico paradosso che, per molti, non è ancora stato risolto. Ma è veramente un paradosso o solo una specie di fake news?
A qualcuna/o piacciono i concorsi ippici ? Bene, questo è il quiz che fa per lei/lui ! Attenzione alla seconda domanda che implica una formula risolutrice calcolata "a priori".
Andiamo verso fake news scientifiche (matematiche soprattutto) partendo dal grande Totò.
Il vostro contachilometri è rotto, ma le pietre miliari vi possono indicare la velocità.
Questo breve articolo vuole essere l'introduzione a un argomento che caratterizza sempre più la nostra esistenza: le fake news. In un mondo in cui l'ignoranza sta diventando sempre più un pregio piuttosto che un difetto, la capacità di distinguere le notizie vere da quelle false è sempre più arduo. Noi, però, vogliamo trattare l'argomento da un punto di vista "scientifico", ossia occuparci dei cosiddetti "paradossi" che potremmo facilmente trattare come fake news, dato che, in fondo, inseriscono "errori" o "ambiguità" all'interno di processi apparentemente logici e realistici.
Un calendario molto semplice e un quiz alla portata di tutti, tanto per riprendere dimestichezza con i quiz e con il ragionamento. I più esperti aspettino un paio di giorni...
Questo articolo cosituisce un "intermezzo" necessario a fornire strumenti utili per la prosecuzione dello studio degli infiniti di Cantor
Se le infinite stanze dell'hotel "Hilbert" non sono sufficienti, ci si può trasferire da Cantor...
Affermiamo intanto che un insieme è finito se riusciamo a contare il numero dei suoi elementi. Tale numero è proprio la cardinalità dell'insieme.