Adesso che abbiamo introdotto il concetto di insieme, vediamo come legare fra loro due insiemi.
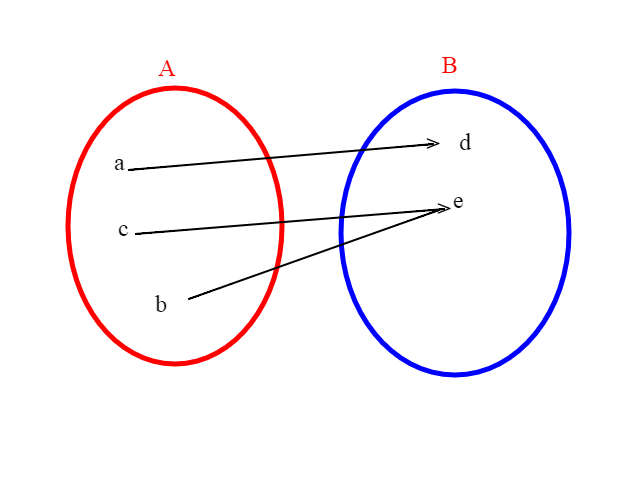

Adesso che abbiamo introdotto il concetto di insieme, vediamo come legare fra loro due insiemi.
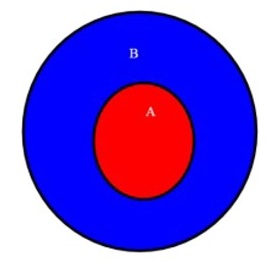
Già nell'antica Grecia era noto il concetto di infinito, Galileo aveva già compreso a quali paradossi può portare, ma la formulazione matematica rigorosa è dei tempi moderni (circa nel 1878) ed è dovuta a Georg Cantor. Il grande matematico David Hilbert disse di lui: « Nessuno riuscirà a cacciarci dal Paradiso che Cantor ha creato per noi. »

Fabrizio è stato bravissimo a risolvere il quiz. Leggete attentamente la soluzione che riporto e faremo un bel ripasso di italiano...

Chi ha la mia età si ricorderà sicuramente questa canzoncina inserita in modo ossessivo nel film di Fellini "Le tentazione del Dott. Antonio" mentre dilagavano le prosperose forme di Anita Ekberg. Chi non l'ha mai visto cerchi di trovarlo sulla rete: ne vale la pena. Il film, oltretutto, è solo un episodio dei quattro che compongono Boccaccio '70.
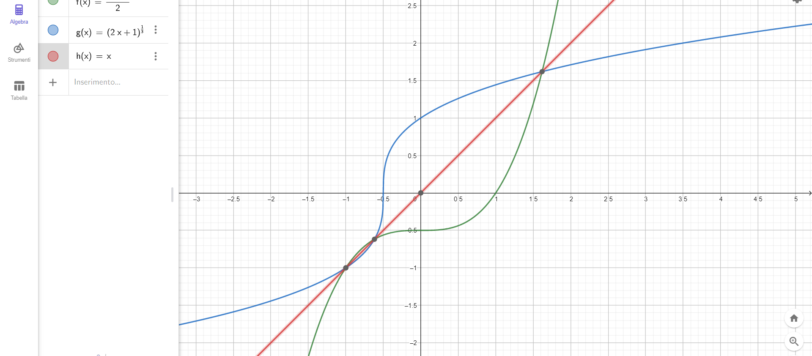
Un quiz non proprio banale che abbisognava soprattutto di un po' di fantasia e di riflessione. Andy l'ha risolto brillantemente ed è stato insignito, da me medesimo, del titolo prestigioso di Primo Matematico del Circolo.

Un problema che appare piuttosto difficile, ma che, alla fine, si dimostra molto più facile del previsto. Dopo qualche quiz decisamente elementare, presentiamone uno un po' più complicato.
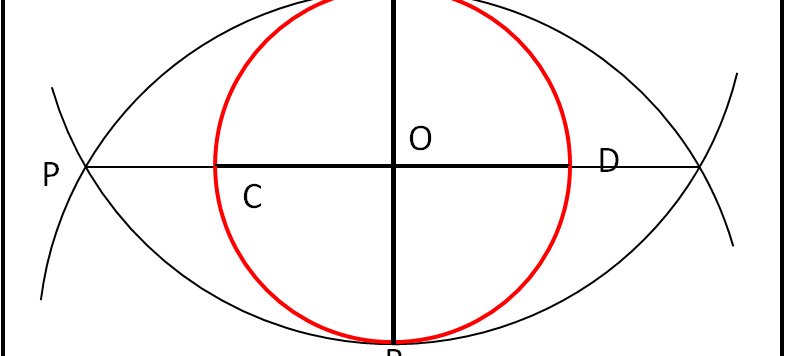
Concludiamo la nostra analisi dei metodi "approssimati" che ci permettono di disegnare qualsiasi poligono regolare di n lati.
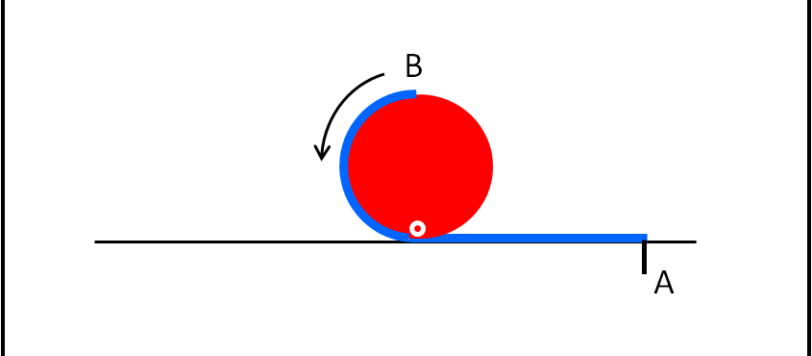
Due monete rotanti riescono a creare più di un paradosso che, però, possono essere risolti e/o prevenuti in qualsiasi caso, senza bisogno di formule.

In attesa della fine dell'anno, eccovi un altro piccolo quiz, che ha -forse- una storia segreta alle spalle..
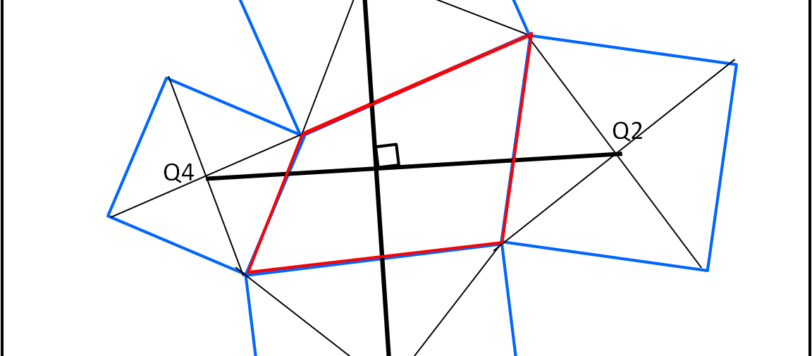
Rinfrescata la memoria sulle proprietà della somma e differenza di vettori, affrontiamo un interessantissimo problema che, nuovamente, potrebbe essere stato enunciato dagli antichi greci. Invito caldamente i più esperti, in attesa del cenone di Capodanno, a tentare di dare la soluzione in modo autonomo, magari indicandomela nei commenti. Vi assicuro che è un bellissimo gico geometrico!

La difficoltà di questo quiz geometrico sta -forse- in una soluzione che potrebbe sembrare controintuitiva. Dopo di che basta il semplice teorema di Pitagora...
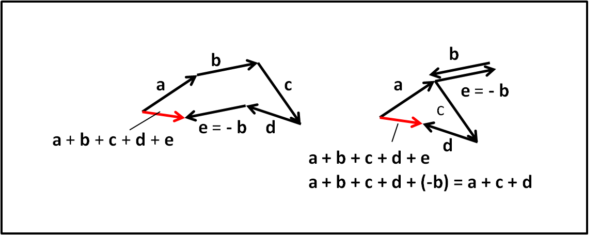
Questo articolo è decisamente elementare e descrive qualche "ovvia" proprietà della somma di vettori. Lo scopo finale, però, va oltre una semplice descrizione, dato che permette di avere le basi per affrontare un teorema poco noto, ma decisamente interessante. Un modo per evidenziare come la matematica e la geometria siano materie tutt'altro che aride e prive di emozioni.