Attenzione alla bambola russa ...
Tre sfere di raggio diverso permettono un simpatico problema dalla soluzione forse inaspettata.
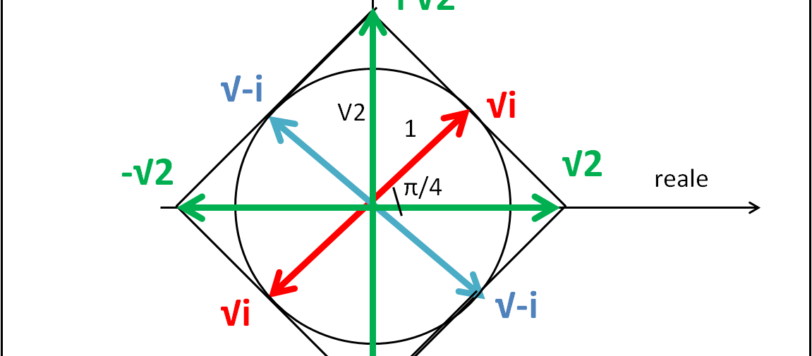
Giochiamo un po' con l'unità immaginaria i senza dimenticare soluzioni per strada ed escludendo fraintendimenti...
No, non sono diventato matto (o, almeno, lo spero), ma lasciatemi porre questa domanda, aspettandomi risposte anche dai più esperti.
un simpatico quiz più logico che matematico alla portata di tutti. Bisogna però ragionarci un po' sopra ...
La successione di Catalan, ovvero... anche Eulero può trovarsi in difficoltà.
Un esempio semplice di calcolo con i numeri complessi. Semplice sì, ma da prendere con le dovute cautele...
Un quiz che può essere risolto anche a ... pancia piena!
Il tutto si riduce alla soluzione di qualche equazione di secondo grado. Basta saperle scegliere...
Un'equazione non banale... ma lo è proprio?
Riporto le soluzioni in un articolo a parte vista la lunghezza non indifferente... L'approccio cinematico è molto simile a quello di Fabrizio. Inoltre, trovate anche la soluzione analitica (riassunta nel commento di Fabrizio) che rappresenta di per sé un approccio più laborioso, ma altrettanto istruttivo.
Un bel problemino di cinematica "quasi" elementare. Provate a risolverlo e fra un paio di giorni aggiungerò la(e) soluzione(i).
Non so quanti leggeranno la quarta e ultima parte del Problema di Apollonio. Forse è considerata del tutto inutile e fine a se stessa. Non lo è, ma, anche se lo fosse, non dimentichiamoci che la "geometria" può diventare una forma d'arte e anche l'arte non ha un interesse veramente pratico. Non si vive di solo pane...
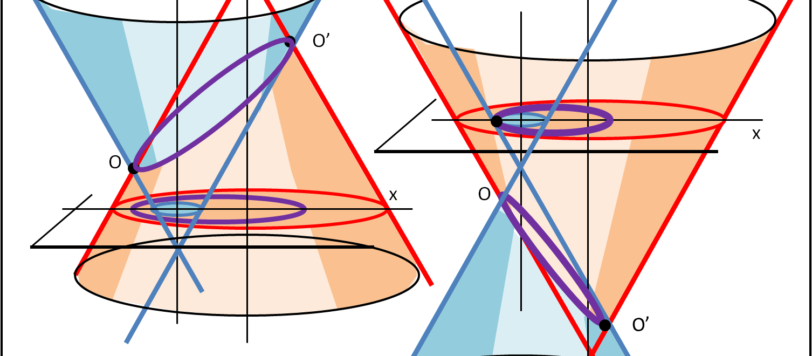
Trattiamo il caso in cui le due circonferenze sono una interna all'altra: le iperboli diventano ellissi.
continuiamo a tracciare i centri delle circonferenze tangenti a quelle di partenza, rimanendo sempre nel caso che queste ultime siano esterne una all'altra.
Un grillo innamorato, timoroso dell'acqua, sfrutta le foglie galleggianti su un fiume per raggiungere la sua amata "grilla". Potendo fare o un salto breve o uno lungo quanti possibili percorsi può fare? Fibonacci saprebbe rispondere, ma molto prima di lui lo aveva già fatto Virahanka!