Un quiz che ha ottenuto poco successo, ma che ha visto la risposta qualitativamente esatta di Daniela. Direi che vale la pena, comunque, di darne anche il risultato quantitativo.
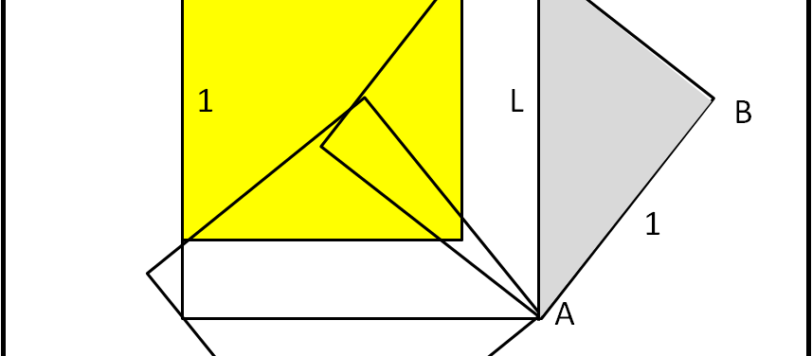

Un quiz che ha ottenuto poco successo, ma che ha visto la risposta qualitativamente esatta di Daniela. Direi che vale la pena, comunque, di darne anche il risultato quantitativo.
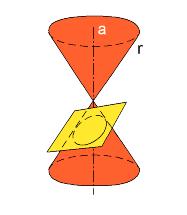
Questo articolo non è un quiz, ma una richiesta di collaborazione nel pieno spirito del nostro Circolo. L'argomento è ancora quello delle costruzioni geometriche dei greci ed in particolare della Scuola di Atene.

Un bel problema di geometria che abbisogna di un certo intuito e molto ragionamento. Affrontiamolo senza chiedere aiuto allo studio di funzioni, ma solo a un'analisi attenta di quello che abbiamo e di ciò che vogliamo trovare.

Come previsto, noi non siamo certo milioni, ma malgrado le ferie abbiamo superato il limite... Un quiz nato a fine ottocento che ha visto la partecipazione di milioni e milioni di appassionati. Oggi, temo che il numero delle risposte esatte diminuirebbero di molto, tranne che da noi...

Abbiamo imparato in modo molto schematico, ma sufficiente allo scopo, a disegnare ciò che il nostro occhio vede. Esso vede tutto proiettato su un piano e in tale piano tutte le linee parallele devono convergere in un punto. In altre parole, abbiamo introdotto la prospettiva centrale, ossia quella forse più ovvia e comune. Attraverso di lei è possibile finalmente creato uno spazio reale in cui inserire, come volumi ben definiti, anche le figure siano esse oggetti, edifici o anche persone. Il Rinascimento insegna...

Dopo il coltello del calzolaio, Archimede introduce, nel lemma 14, anche la saliera (Salinon). il nome deriva sicuramente dalla forma, anche se vi sono altre ipotesi in proposito.
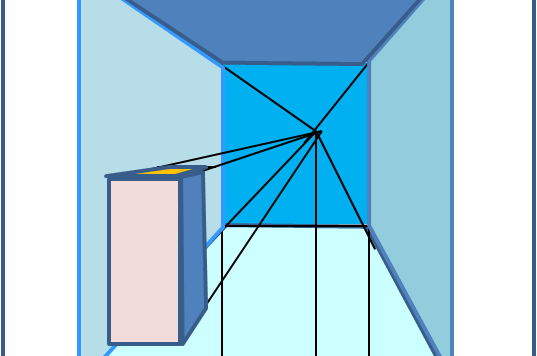
Risolviamo il piccolo problema legato al pentagono e poi passiamo alla rappresentazione di un solido. Il Rinascimento si avvicina sempre di più...

Non è banale raggiungere e riuscire a visitare la Cappella degli Scrovegni a Padova, ma quella del nostro quiz è ancora più difficile da raggiungere.
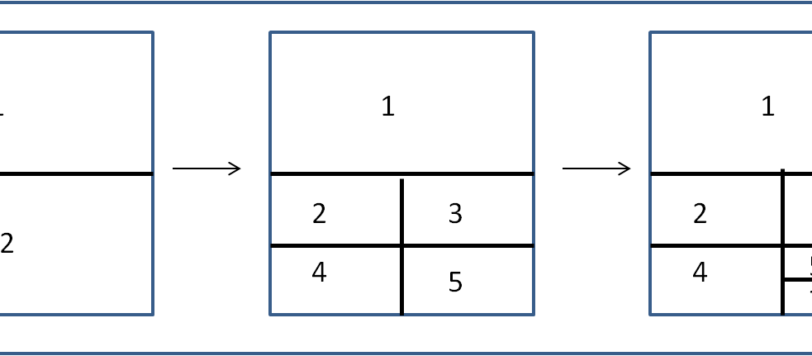
Una soluzione forse inaspettata, ma , in fondo, bastano due procedure per avere la sicurezza. Un po' più di fantasia è necessaria per risolvere un caso apparentemente impossibile.
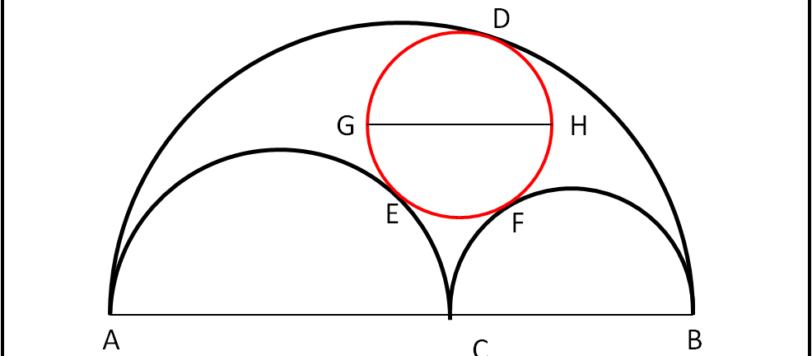
Continuiamo a divertirci con il nostro "arbelos" e a scoprire alcune delle sue innumerevoli proprietà.
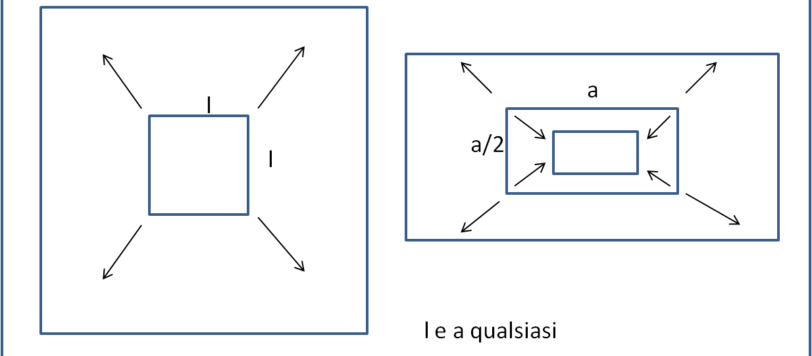
Un problemino non certo difficile, ma che comporta una buona dose di ragionamento e di ... fantasia.