Prendiamo spunto dall'intrigante problema della capretta legata a una corda per ricordare un paradosso di Zenone, Blade Runner, una rana in miniatura e un'equazione trascendente.
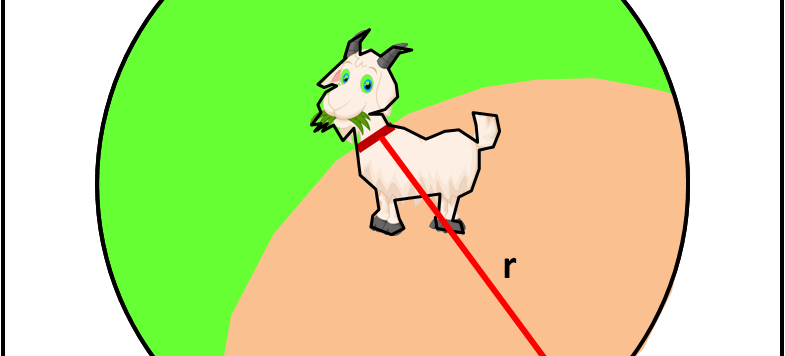

Prendiamo spunto dall'intrigante problema della capretta legata a una corda per ricordare un paradosso di Zenone, Blade Runner, una rana in miniatura e un'equazione trascendente.
Cari amici, come avete notato sia Umberto che Maurizio non scrivono più per noi. Tuttavia, per chi volesse continuare a seguire la trattazione accurata della matematica pura (e non solo) riporto il link al nuovo blog di Umberto... A PROPOSITO
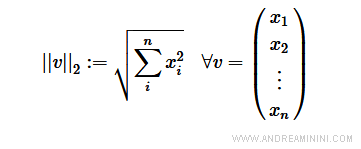
Una breve precisazione che tornerà utile nel prosieguo dell'analisi della relatività generale...
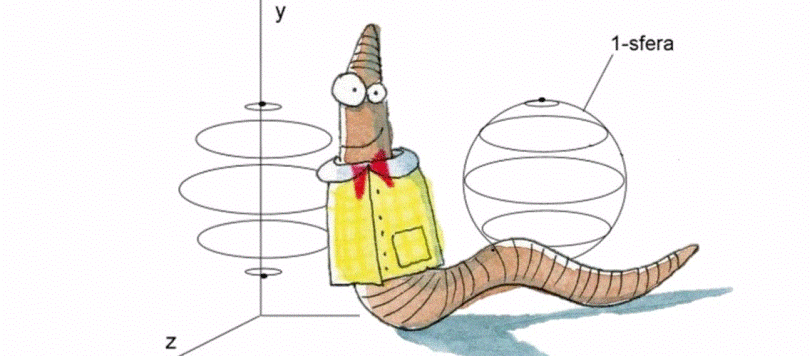
Ci uniamo alle celebrazioni del settecentenario della morte di Dante Alighieri, riproponendo un progetto di cui andiamo molto fieri, nel quale letteratura, storia e scienza si intrecciano lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna: un entusiasmante viaggio al termine del quale dimostreremo, tramite l'analisi dei suoi stessi versi, la capacità del Sommo Poeta di immaginare una struttura teologica e scientifica ben al di là dei suoi tempi, anticipando di fatto la visione matematica di Riemann e quella fisica di Einstein.

Cari amici, la generalizzazione del problema iniziale mi ha portato a cercare una nuova strada per descrivere il "fenomeno" geometrico. Una strada che mi è sembrata molto interessante e, all'apparenza almeno, del tutto inesplorata. Il bello è che potrebbe essere resa benissimo da una animazione (vero Arturo?) o permettere di costruire un qualche aggeggio concreto (vero Frank?). Fatemelo dire: possiamo chiamarlo "l'ultimo (ma anche il primo!) teorema di Zappalà o, meglio, di Zappalat" e che Fermat non me ne voglia!

Il quiz dei due cerchi, "incatenati" al triangolo equilatero, sembra aver perso di interesse. Peccato... perché proprio la seconda parte è quella più interessante, che ci permette addirittura di enunciare un "nuovo" teorema, simile a tanti ricavati dai greci antichi. A quanto mi risulta non mi sembra che sia mai stato enunciato, ma potrei sbagliarmi. Comunque un piccolissimo tassello geometrico in più del nostro circolo.

Riporto la soluzione della prima parte, ma lascio ancora in sospeso la seconda parte, quella più "giapponese". Il quiz, quindi, continua.

In questo articolo descrivo la realizzazione di un modello di geometria solida con il quale ho voluto verificare il funzionamento di una montatura equatoriale, ossia un particolare sostegno di un telescopio molto utilizzato in ambito amatoriale e non solo. La montatura equatoriale consente con un unico movimento, manuale o motorizzato, di "inseguire" il moto apparente di un astro nel cielo, in realtà ruotando in sincrono col moto di rotazione terrestre.
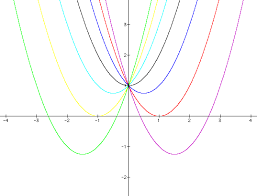
In realtà, risolvere un'equazione di secondo grado non è difficile. L'unico problema può essere, per qualcuno, ricordare a memoria la formula risolutiva. Ma è veramente necessario? Rifacendosi in parte ai babilonesi, possiamo dire di NO.

E' un periodo che sforno tanti quiz e sono contento di vedere che riscuotono successo. Anzi, mi accorgo che, a volte uno a volte un altro, siete prontissimi a rispondere. Voglio provare a divertirmi anch'io, sicuro della vostra partecipazione!

L'ipotesi della natura corpuscolare della luce si fa solitamente risalire a Newton. Ma non è così! Basterebbe avere meno "campanilismo" scientifico...

E' successo quello che "doveva" succedere... questo quiz l'avevo già proposto nel 2018, ma me ne ero completamente dimenticato. Il nostro Arturo Lorenzo se n'è accorto subito, ma abbiamo deciso di non rimuoverlo, dato che i nuovi arrivi sono stati molti.

Eccovi la soluzione, perfettamente individuata da Fabrizio, prima, e da Gianfranco dopo. Per non parlare di Leandro che ha perfino introdotto un aiuto di tipo "fisico" per aiutare il nostro fratello scansafatiche. Tuttavia, non si pretendeva tanto e quindi limitiamoci alla soluzione puramente "matematica".

Un quiz che può anche essere considerato facile, ma che può, facilmente, diventare veramente diabolico. Per risparmiare molta fatica mentale -e non solo fisica- basta infatti ben poco... Tutto sta nello scegliere l'approccio giusto.

I giapponesi, oltre a tutti i loro misteri, i loro riti, le loro cerimonie, il loro modo di pensare e agire, ben diverso da quello occidentale, ci hanno anche regalato una geometria del tutto speciale, veramente affascinante. Iniziamo a entrare in questo mondo, dove intendo tornare spesso ...