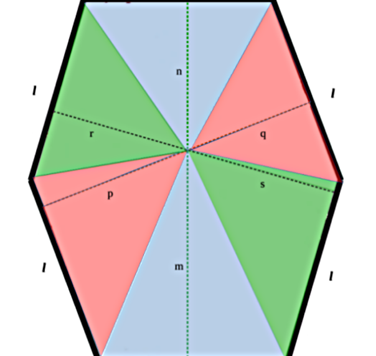
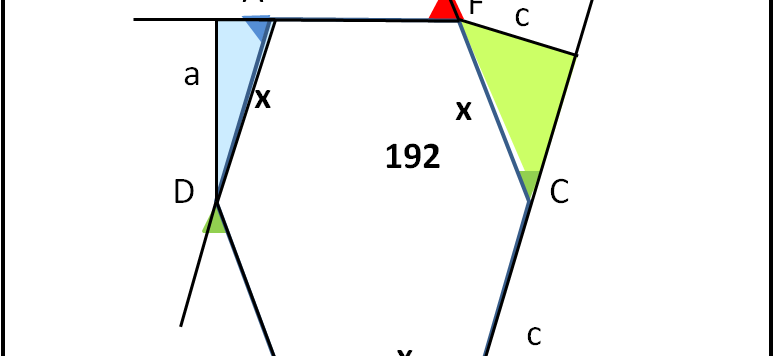
E' bello scoprire anche aspetti artistici e geometrici in ciò che avviene nell'Universo. Nei giorni scorsi, desideroso di avere un mio modello geometrico da cui ricavare in qualsiasi momento la distanza tra Venere e la Terra, ho implementato nel solito software Geogebra le orbite dei due pianeti. Ecco a voi il risultato!