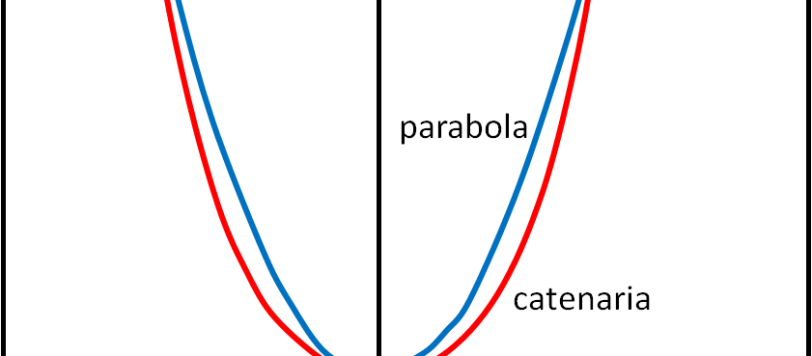
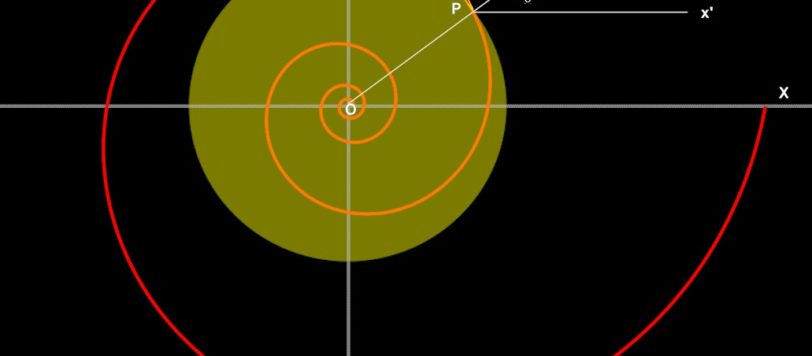
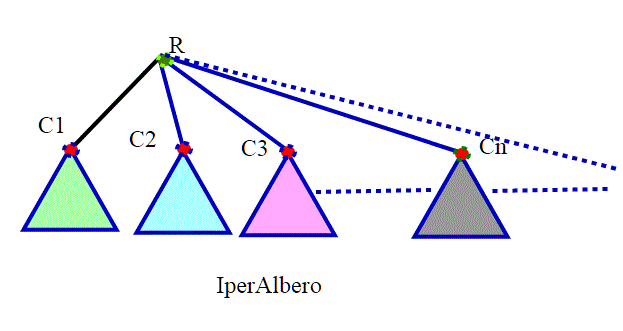
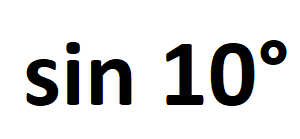La prima volta che ho visto questo problema, a cui sinceramente non ho dato molta importanza, è stato su un sito in lingua inglese; tutti conoscono il traduttore automatico di google, che a volte parte appunto da solo e traduce in italiano. Ho pensato : ma cosa c'entra questo con la matematica? L'ho poi ritradotto […]