Questa volta voglio accontentare i più bravi ed ecco un bel quiz matematico con quattro asterischi che possono anche diventare sei per i bravissimi (e molto fantasiosi).


Questa volta voglio accontentare i più bravi ed ecco un bel quiz matematico con quattro asterischi che possono anche diventare sei per i bravissimi (e molto fantasiosi).

Concludiamo l'avventura di Tarzan sia matematicamente che geometricamente, permettendo anche una costruzione meccanica (roba da ingegneri della giungla...)

Ebbene sì... proviamo finalmente a definire in modo molto semplificato (spero) il fantomatico "tensore" che tanta paura esercita in chi cerca di avvicinarlo. Lo facciamo in modo forse meno convenzionale, cercando di affrontarlo da un punto quasi puramente geometrico, sperando che i due asterischi diano la giusta quantificazione della sua effettiva difficoltà (ossia è articolo per TUTTI coloro che si sentano di dare del tu ai vettori). Pensiamo che sarà poi più semplice capirne le proprietà che lo rendono anche un "oggetto" di pura matematica. Inoltre, cerchiamo anche di approfittare di questa introduzione per capire ancora meglio sia l'importanza e la genialità concettuale della Relatività Generale, sia la difficoltà estrema che si cela dietro una formula finale dall'apparenza molto innocua.
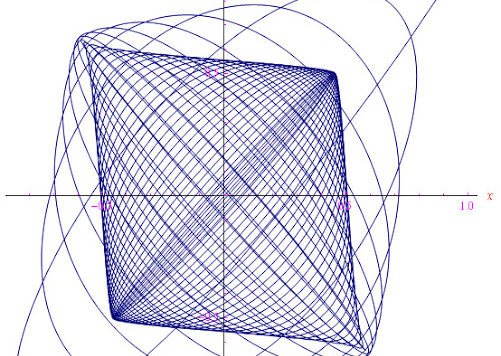
In questa prima parte torniamo un po' all'antica... ai bei tempi in cui cercavo di spiegare l'analisi matematica, con tanto di derivate e integrali, in modo comprensibile a tutti coloro dotati di voglia di imparare e di conoscere, per avendo basi di partenza molto basse (che male c'è?). Iniziamo perciò in modo veramente elementare e ci portiamo rapidamente e facilmente a maneggiare le celebri e bellissime figure di Lissajous. Per far contenti coloro che usano dire: "Sì, belle... ma a che servono?" toccheremo le applicazioni che le hanno portate ad essere fondamentali nel posizionare velivoli spaziali che necessitano di condizioni stabili e non vicinissime alla Terra. E se ce la sta facendo l'uomo, potete giurarci che non se l'è certo fatto scappare madre Natura!

La soluzione del quiz è stata trovata da molti, in modo più o meno diverso. Alcuni hanno scelto la via meno banale, altri no. Essenzialmente vi sono due modi per risolvere la questione. Uno di carattere empirico (che avrebbe bisogno di una verifica anche se è molto intuitivo) e uno legato al calcolo combinatorio. La […]

Niente da fare... Arturo e Fabrizio sono delle macchine schiacciasassi, anzi schiacciaquiz! Rapidi, precisi e infallibili. Soprattutto ammiro la loro fantasia e la chiarezza delle risposte, che permettono di proseguire nell'analisi dei risultati e allargare il campo anche in un algebra apparentemente elementare, ma piena di risvolti imprevisti. La matematica, in fondo, può anche divertire! Mi sono di grande aiuto in questo momento... Tuttavia, devo riuscire a metterli in difficoltà! Forza amici lettori cercate di essere più veloci o, magari, ancora più precisi e fantasiosi. Un premio speciale a chi riuscirà a batterli come, in fondo, è riuscito a fare Marco... Latita Mau, ma è sicuramente impegnato in altre faccende insieme al suo amico Oreste. Lui è un altro che non perdona! Per chi volesse far scendere un po' la difficoltà vi è un aiuto nascosto al fondo dell'articolo. Non lo guarderanno certo i nostri super eroi..

Visto il rapido successo dell'ultimo quiz senza l'uso del calcolatore o di una qualsiasi calcolatrice, ve ne propongo subito un altro, forse leggermente più difficile... Magari troverete un metodo più rapido del mio... non mi stupirei di certo!

Sto vedendo che i quiz semplici mietono poco successo. Va bene... presentiamone uno che potrà interessare anche i più bravi in matematica (ma tutti possono provare a risolverlo). Bisogna calcolare un'espressione SENZA utilizzare computer o calcolatrici, solo carta e penna, un minimo di algebra e ... facilissimi calcoli mentali (basta la tabellina pitagorica).

Chi ha un po' di anni come me non può non ricordare Gigi Riva, detto Rombo di Tuono, capace di dare un contributo essenziale alla vittoria dello scudetto del Cagliari (squadra che non ha mai lasciato) nel 1969-70. Ala sinistra formidabile, era un vero flagello per le squadre avversarie e i suoi goal tantissimi anche da posizioni non proprio perfette. Eh sì... per un ala sinistra (o destra) è necessario conoscere un po' di trigonometria o -almeno- un po' di geometria.

Che Riemann non scherzasse affatto con le sue innovazioni è cosa certa; non tutti però conoscono Lebesgue, che fu un personaggio forse non troppo di rilievo nella matematica recente (recente per modo di dire), ma che spianò la strada per una matematica che forse ha i più efficaci risvolti in fisica non classica.
IL quiz, che trovate qui , richiedeva di dimostrare che il sin10° è un numero irrazionale. Come detto nell'introduzione al quiz, esso era dedicato agli amanti della trigonometria, che invece io uso solo per stretta necessità. In ogni caso, ritengo che anche chi conosca appena la materia, ricordi a memoria la formula di addizione degli […]

Beh... a scanso di equivoci vi dico subito che il seno in questione è la ben nota funzione trigonometrica e che gli "indiani" sono proprio gli abitanti dell'India.

E' piuttosto strano che a un quiz con tanti asterischi si possa rispondere con due soli asterischi. Il motivo è, però, semplice: il quiz non ha ancora una soluzione!
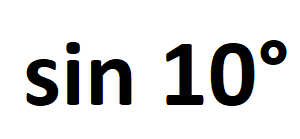
La prima volta che ho visto questo problema, a cui sinceramente non ho dato molta importanza, è stato su un sito in lingua inglese; tutti conoscono il traduttore automatico di google, che a volte parte appunto da solo e traduce in italiano. Ho pensato : ma cosa c'entra questo con la matematica? L'ho poi ritradotto […]
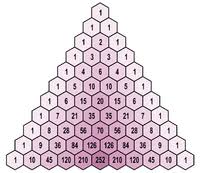
Grazie a Fabrizio e Maurizio, ci siamo liberati di un problema non proprio banale, che consisteva nel trovare il numero di cifre di una potenza: Fabrizio ha proprio fatto ciò che intendevo io, quando nel testo mi riferivo come suggerimento nascosto al binomio di Newton. Ritengo questa soluzione quella più precisa, che richiede meno approssimazioni […]