Una domanda estremamente semplice che necessita di una risposta non altrettanto semplice, anche se alla portata di molti.


Una domanda estremamente semplice che necessita di una risposta non altrettanto semplice, anche se alla portata di molti.

Questo articolo va ben oltre il teorema di Tolomeo e introduce una interessantissima trasformazione che si applica al piano euclideo. La sua importanza è enorme in quanto riesce a semplificare molti problemi geometrici, tra cui dare una dimostrazione quasi "ridicola" del teorema di Tolomeo. L'affronteremo solo superficialmente, ma quanto dovrebbe bastare a comprenderne i risvolti più nascosti e generali. Alla fine scriverò una delle mie solite esternazioni e mi aspetto commenti e critiche più che giustificate... Insomma, non perdetevi questo articolo e non consideratelo solo una piccola tessera legata al grande genio di Tolomeo.
Beh... cari amici, devo dire che il nostro Oreste Pautasso ha cercato veramente di presentarci tutti i 54 metodi di risoluzione della prima parte. Abbiamo dovuto abbatterlo dall'albero su cui si era rifugiato per farlo smettere. Ovviamente, per partito preso e per alto senso democratico, nessuno dei suoi metodi può essere considerato "elegante" come quello che avevo in mente io!
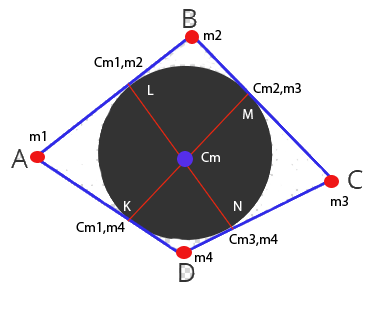
Posso dire di essere molto contento, in quanto quello che desideravo si è avverato; lo scopo era trovare una soluzione alternativa ad un problema molto importante per introdurre la teoria di Ramsey nel piano Euclideo. Ringrazio dunque Vincenzo per essere riuscito in tale intento; il problema non è banale anche se le soluzioni sono semplici. […]

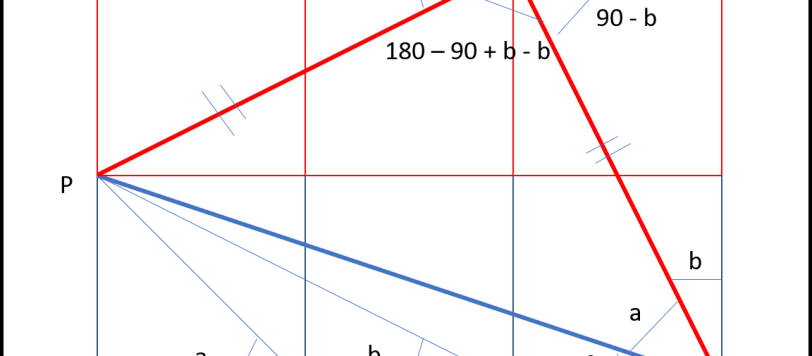
Questo articolo ci mostra come l'applicazione del teorema di Tolomeo porta alla determinazione di due tra le più utilizzate formule di trigonometria.
Un doppio quiz, a due livelli. La prima parte si può risolvere in moltissimi modi. Un prestigioso regalo a chi darà la risposta più "elegante" (a mio giudizio, ovviamente!).

Esiste una classe di affascinanti problemi , nell'ambito del piano o dello spazio, in cui i punti sono contraddistinti da determinate proprietà. Vedremo come questo quesito potrà servire per introdurre una importante classe di problemi di matematica discreta. Tanto per essere originali, assegneremo, ad ogni punto del piano, il metallo di cui è costituito. Diciamo che […]

La geometria, anche quella più semplice, può diventare un vero spettacolo. Soprattutto se c'è di mezzo Tolomeo, grandissimo scienziato, troppo spesso associato solo alla sua visione eliocentrica dell'Universo.

La soluzione è stata più laboriosa del previsto... tuttavia, ringrazio tutti coloro che hanno provato. Il numero 70 girava, ma quasi sempre con un ragionamento non coretto del tutto.
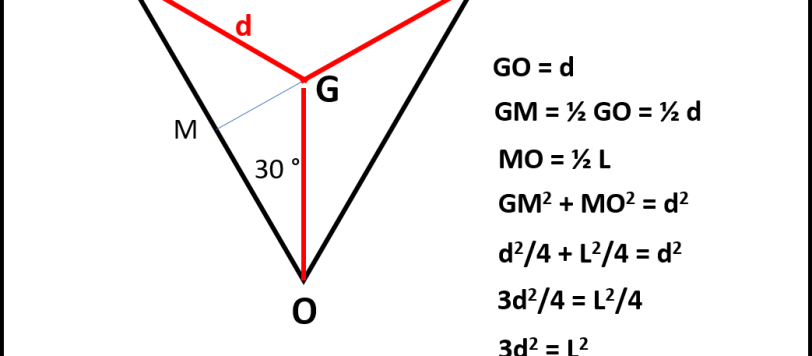
La soluzione da me proposta si basa sulle proprietà del baricentro. Si potrebbe scrivere in modo molto stringato, ma cerco di spiegarla in modo che anche in non esperti in certe proprietà vettoriali del baricentro possano comprenderla. La fisica qui non c'entra niente; lo stesso si avrebbe definendo una certa entità con operazioni da svolgere su vettori con moduli proporzionali a determinati numeri ( numeri detti anche scalari).

Questo quiz di logica più che di matematica è stato letteralmente "sbranato" da Maurizio e nessuno (tranne Ale) ha avuto la voglia di cimentarsi. Cercheremo, la prossima volta, di mettere il bavaglio al nostro Mau... che di questi quiz, relativamente semplici, ne fa un solo boccone!

Un quiz di tanta logica e di poca matematica. Malgrado le apparenze, tutti possono riuscire a risolverlo.
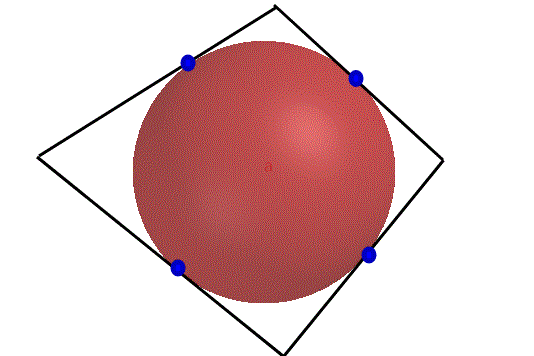
Sto cercando disperatamente di proporre dei quiz che siano risolvibili anche dal cellulare, quindi privi di disegni e calcoli complessi. Lasciamo per un pò perdere poi l'esposizione romanzesca, per essere più precisi, come lo vuole la matematica (anche perchè in questo caso non avrei idee per scriverla). Abbiamo a che fare con una figura sbilenca è una simmetricamente perfetta; cosa succederà ai punti di contatto se si tenta di incastrare una nell'altra?
Un articolo un po' più tecnico dei precedenti, che purtroppo presuppone la conoscenza delle derivate. Tuttavia ciò ci permetterà di sfatare definizioni e formalismi tipici della geometria differenziale, quali i tensori metrici e gli elementi di linea infinitesimi. Ricordiamoci che il nostro scopo è quello di capire come vivere all'interno di una varietà dove di euclideo resta ben poco. In ogni caso, però, tramite il piano tangente possiamo ridurci sempre ad esso.

Questo articolo è estremamente interessante e l'argomento ben poco analizzato (finora almeno). Probabilmente apre un nuovo "mondo" di studi. Leggetelo, quindi, con molta attenzione e mettetevi alla prova. Come forse avrete immaginato, il riferimento al golf non è così forte come si sarebbe potuto credere. Lo scopo era di scuotere un po' il nostro Frank sempre in lotta per scalare posizioni (e anche per prenderci un po' in giro). Che anche lui "scenda" al nostro livello, forse un po' troppo teorico per un tecnogolfista...